Các Phân Phối Xác Suất Thông Thường
Bài tổng quan này chứa nhiều kiến thức quan trọng. Hãy tìm hiểu sự khác biệt giữa phân phối xác suất rời rạc và liên tục. Phân phối nhị thức và phân phối chuẩn là những phân phối quan trọng nhất ở đây. Bạn cần học các thuộc tính của cả hai phân phối và ghi nhớ các công thức cho xác suất của một giá trị cụ thể khi được đưa ra phân phối xác suất nhị thức. Tìm hiểu rủi ro thâm hụt là gì và cách tính toán và sử dụng tiêu chuẩn an toàn của Roy. Biết cách chuẩn hóa một biến ngẫu nhiên phân phối chuẩn, sử dụng bảng z, và xây dựng khoảng tin cậy. Những kỹ năng này sẽ được sử dụng lặp lại trong các bài tổng quan chủ đề tiếp theo. Ngoài ra, hãy hiểu các đặc điểm cơ bản của phân phối lognormal, mô phỏng Monte Carlo và mô phỏng lịch sử. Cuối cùng, sẽ là một ý tưởng tốt nếu biết cách nhận được tỷ suất sinh lời kép liên tục từ các khoản hoàn vốn kỳ hạn.
1: PHÂN PHỐI ĐỀU VÀ PHÂN PHỐI NHỊ THỨC
A: Định nghĩa phân phối xác suất và phân biệt giữa các biến ngẫu nhiên rời rạc và liên tục và các hàm xác suất của chúng.
B: Mô tả tập hợp các kết quả có thể có của một biến ngẫu nhiên rời rạc được chỉ định.
Một phân phối xác suất mô tả xác suất của tất cả các kết quả có thể có cho một biến ngẫu nhiên. Các xác suất của tất cả các kết quả có thể có phải cộng lại bằng 1. Một phân phối xác suất đơn giản là phân phối cho một lần tung một con xúc xắc công bằng; có sáu kết quả có thể có và mỗi kết quả có xác suất là 1/6, vì vậy chúng cộng lại bằng 1. Phân phối xác suất của tất cả các khoản hoàn vốn có thể có trên Chỉ số S&P 500 cho năm tới là một phiên bản phức tạp hơn của cùng một ý tưởng.
Một biến ngẫu nhiên rời rạc là một biến mà số lượng kết quả có thể có thể được đếm, và đối với mỗi kết quả có thể có, có một xác suất đo lường và dương. Một ví dụ về biến ngẫu nhiên rời rạc là số ngày mưa trong một tháng nhất định, vì có một số lượng kết quả có thể đếm được, từ không đến số ngày trong tháng.
Một hàm xác suất, ký hiệu là , xác định xác suất rằng một biến ngẫu nhiên bằng một giá trị cụ thể. Nói một cách chính xác hơn, là xác suất rằng biến ngẫu nhiên nhận giá trị , hay .
Hai tính chất chính của hàm xác suất là:
- .
- , tổng của các xác suất cho tất cả các kết quả có thể, , cho một biến ngẫu nhiên, , bằng 1.
Xét hàm sau: , , còn lại thì
Xác định xem hàm này có thỏa mãn các điều kiện của một hàm xác suất hay không.
Trả lời:
Lưu ý rằng tất cả các xác suất đều nằm trong khoảng từ 0 đến 1, và tổng của tất cả các xác suất bằng 1:
Cả hai điều kiện cho một hàm xác suất đều được thỏa mãn.
Một biến ngẫu nhiên liên tục là biến có số kết quả có thể là vô hạn, ngay cả khi có tồn tại các giới hạn dưới và trên. Lượng mưa hàng ngày thực tế giữa không và 100 inch là một ví dụ về biến ngẫu nhiên liên tục vì lượng mưa thực tế có thể có vô số giá trị. Lượng mưa hàng ngày có thể được đo bằng inch, nửa inch, phần tư inch, phần nghìn inch, hoặc thậm chí nhỏ hơn. Do đó, số lượng các lượng mưa hàng ngày có thể xảy ra giữa không và 100 inch là vô hạn.
Việc gán xác suất cho các kết quả có thể cho các biến ngẫu nhiên rời rạc và liên tục cung cấp cho chúng ta các phân phối xác suất rời rạc và phân phối xác suất liên tục. Sự khác biệt giữa các loại phân phối này rõ ràng nhất ở các tính chất sau:
-
Đối với phân phối rời rạc, khi không thể xảy ra, hoặc nếu nó có thể. Nhớ rằng được đọc là: “xác suất rằng biến ngẫu nhiên .” Ví dụ, xác suất trời mưa 33 ngày trong tháng Sáu là không vì điều này không thể xảy ra, nhưng xác suất trời mưa 25 ngày trong tháng Sáu có giá trị dương.
-
Đối với phân phối liên tục, ngay cả khi có thể xảy ra. Chúng ta chỉ có thể xem xét nơi mà và là các số thực. Ví dụ, xác suất nhận được hai inch mưa trong tháng Sáu là không vì hai inch là một điểm duy nhất trong một dải vô hạn các giá trị có thể. Mặt khác, xác suất lượng mưa nằm trong khoảng từ 1.999999999 đến 2.000000001 inch có giá trị dương. Trong trường hợp của các phân phối liên tục, vì .
Trong tài chính, một số phân phối rời rạc được coi như liên tục vì số lượng kết quả có thể rất lớn. Ví dụ, sự tăng hoặc giảm giá của một cổ phiếu được giao dịch trên một sàn giao dịch Mỹ được ghi lại bằng đô la và xu. Tuy nhiên, xác suất của một thay đổi chính xác là $1.33 hoặc $1.34 hoặc bất kỳ thay đổi cụ thể nào khác gần như bằng không. Vì vậy, thường nói về xác suất của một dải thay đổi giá có thể, chẳng hạn như giữa $1.00 và $2.00. Nói cách khác, gần như bằng không, nhưng lớn hơn không.
C: Diễn giải hàm phân phối tích lũy.
D: Tính toán và diễn giải xác suất cho một biến ngẫu nhiên, dựa trên hàm phân phối tích lũy của nó.
Một hàm phân phối tích lũy (cdf), hay đơn giản là hàm phân phối, định nghĩa xác suất rằng một biến ngẫu nhiên, , nhận giá trị bằng hoặc nhỏ hơn một giá trị cụ thể, . Nó đại diện cho tổng, hoặc giá trị tích lũy, của các xác suất cho các kết quả lên đến và bao gồm một kết quả được chỉ định. Hàm phân phối tích lũy cho một biến ngẫu nhiên, , có thể được biểu diễn là .
Hãy xem xét hàm xác suất đã được định nghĩa trước đó cho , . Với phân phối này, , và . Điều này có nghĩa là là xác suất tích lũy rằng các kết quả 1, 2, hoặc 3 xảy ra, và là xác suất tích lũy rằng một trong những kết quả có thể xảy ra.
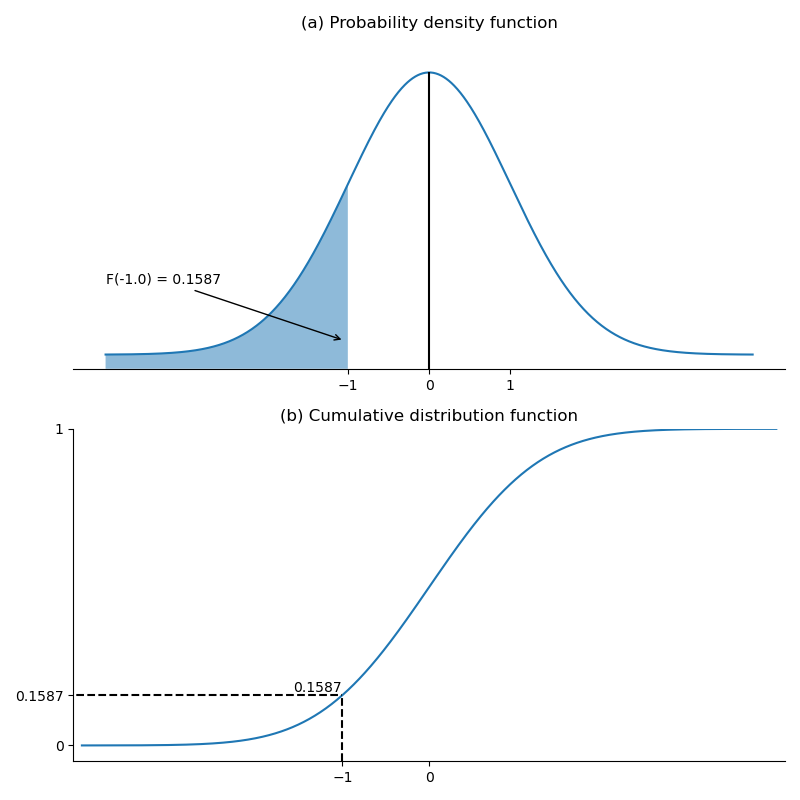
Hình sau đây minh họa một ví dụ về hàm phân phối tích lũy (cho phân phối chuẩn, được mô tả sau trong chủ đề này). Có xác suất 15.87% của một giá trị nhỏ hơn -1. Đây là tổng diện tích bên trái của -1 trong pdf ở hình (a), và giá trị trục y của cdf cho một giá trị của -1 trong hình (b).
Hình: Hàm mật độ xác suất chuẩn và hàm phân phối tích lũy
Lợi nhuận trên vốn chủ sở hữu (ROE) cho một công ty được định nghĩa là một phân phối liên tục trong khoảng từ đến và có hàm phân phối tích lũy là . Tính xác suất rằng ROE sẽ nằm trong khoảng từ đến .
Trả lời:
Để xác định xác suất rằng ROE sẽ nằm trong khoảng từ đến , chúng ta có thể tính xác suất rằng ROE sẽ nhỏ hơn hoặc bằng , hoặc , và sau đó trừ đi xác suất rằng ROE sẽ nhỏ hơn không, hoặc .
E: Định nghĩa biến ngẫu nhiên rời rạc đều, biến ngẫu nhiên Bernoulli và biến ngẫu nhiên nhị thức.
F: Tính toán và giải thích xác suất dựa trên hàm phân phối rời rạc đều và nhị thức.
Một biến ngẫu nhiên rời rạc đều là một biến ngẫu nhiên rời rạc có xác suất cho tất cả các kết quả có thể xảy ra là bằng nhau. Ví dụ, xem xét phân phối xác suất rời rạc đều được định nghĩa là . Ở đây, xác suất cho mỗi kết quả là bằng 0.2 [tức là, ]. Ngoài ra, hàm phân phối tích lũy cho kết quả thứ n, , và xác suất cho một khoảng kết quả là , trong đó là số lượng kết quả có thể trong khoảng đó.
Xác định , , và cho hàm phân phối rời rạc đều được định nghĩa như sau:
Trả lời:
, vì cho tất cả . . Lưu ý rằng vì 6 là kết quả thứ ba trong các kết quả có thể xảy ra. . Lưu ý rằng , vì có bốn kết quả trong khoảng .
| X = x | Xác suất của x (Prob (X = x)) | Hàm phân phối tích lũy (Prob (X < x)) |
|---|---|---|
| 2 | 0.20 | 0.20 |
| 4 | 0.20 | 0.40 |
| 6 | 0.20 | 0.60 |
| 8 | 0.20 | 0.80 |
Hàm phân phối tích lũy cho
Phân phối nhị thức
Một biến ngẫu nhiên nhị thức có thể được định nghĩa là số lần "thành công" trong một số lần thử nghiệm nhất định, trong đó kết quả có thể là "thành công" hoặc "thất bại." Xác suất thành công, , là không đổi cho mỗi lần thử, và các lần thử là độc lập. Một biến ngẫu nhiên nhị thức mà số lần thử là 1 được gọi là biến ngẫu nhiên Bernoulli. Hãy nghĩ về một lần thử như một thí nghiệm nhỏ (hoặc "thử nghiệm Bernoulli"). Kết quả cuối cùng là số lần thành công trong một loạt lần thử. Trong những điều kiện này, hàm xác suất nhị thức định nghĩa xác suất của lần thành công trong lần thử. Nó có thể được biểu diễn bằng công thức sau:
trong đó:
- số cách chọn x từ n = có thể được ký hiệu là hoặc nói là "n chọn x"
- = xác suất của "thành công" trong mỗi lần thử [đừng nhầm lẫn với p(x)]
Vì vậy, xác suất của chính xác lần thành công trong lần thử là:
Giả sử một phân phối nhị thức, tính xác suất rút được ba hạt đậu đen từ một bát đậu đen và đậu trắng nếu xác suất chọn một hạt đậu đen trong bất kỳ lần thử nào là 0.6. Bạn sẽ rút năm hạt đậu từ bát.
Trả lời:
Một chút trực giác về những kết quả này có thể giúp bạn nhớ các phép tính. Hãy xem xét một bát đậu đen và đậu trắng (rất lớn) có 60% là đậu đen và mỗi lần bạn chọn một hạt đậu, bạn thay thế nó vào bát trước khi rút lại. Chúng ta muốn biết xác suất chọn chính xác ba hạt đậu đen trong năm lần rút, như trong ví dụ trước.
Một cách để điều này xảy ra là BBBWW. Vì các lần rút là độc lập, xác suất của điều này rất dễ tính. Xác suất chọn một hạt đậu đen là 60%, và xác suất chọn một hạt đậu trắng là . Do đó, xác suất chọn BBBWW, theo thứ tự, là . Đây là từ công thức và là 60%, xác suất chọn một hạt đậu đen trong bất kỳ lần rút nào từ bát. Tuy nhiên, BBBWW không phải là cách duy nhất để chọn chính xác ba hạt đậu đen trong năm lần thử. Một khả năng khác là BBWWB, và khả năng thứ ba là BWWBB. Mỗi trường hợp này sẽ có xác suất xảy ra chính xác như kết quả ban đầu của chúng ta, BBBWW. Đó là lý do tại sao chúng ta cần trả lời câu hỏi có bao nhiêu cách (thứ tự khác nhau) để chúng ta chọn ba hạt đậu đen trong năm lần rút. Sử dụng công thức, có , là câu trả lời chúng ta đã tính ở trên.
Giá Trị Kỳ Vọng và Phương Sai của Biến Ngẫu Nhiên Nhị Thức
Đối với một loạt thử nghiệm, số lần thành công kỳ vọng, hay , được cho bởi công thức sau:
giá trị kỳ vọng của
Trực giác khá đơn giản; nếu chúng ta thực hiện thử nghiệm và xác suất thành công trong mỗi thử nghiệm là , chúng ta kỳ vọng có lần thành công.
Phương sai của biến ngẫu nhiên nhị thức được cho bởi:
phương sai của
Dựa trên dữ liệu thực nghiệm, xác suất rằng Chỉ số Công nghiệp Dow Jones (DJIA) sẽ tăng vào bất kỳ ngày nào được xác định là 0.67. Giả sử rằng kết quả duy nhất khác là nó giảm, chúng ta có thể nói p(LÊN) = 0.67 và p(XUỐNG) = 0.33. Hơn nữa, giả sử rằng các chuyển động trong DJIA là độc lập (tức là, việc tăng một ngày không phụ thuộc vào điều gì đã xảy ra vào ngày khác).
Sử dụng thông tin đã cung cấp, tính giá trị kỳ vọng của số ngày tăng trong một khoảng thời gian 5 ngày.
Trả lời:
Sử dụng thuật ngữ nhị thức, chúng ta định nghĩa thành công là LÊN, vậy . Lưu ý rằng định nghĩa của thành công là rất quan trọng đối với bất kỳ bài toán nhị thức nào.
Hãy nhớ rằng ký hiệu “|” có nghĩa là cho trước. Do đó, câu nói trước đó được đọc là: giá trị kỳ vọng của cho trước , và xác suất thành công = 67% là 3.35.
Chúng ta nên lưu ý rằng vì phân phối nhị thức là một phân phối rời rạc, kết quả là không thể. Tuy nhiên, nếu chúng ta ghi lại kết quả của nhiều khoảng thời gian 5 ngày, số ngày tăng trung bình (thành công) sẽ hội tụ về 3.35.
Mô hình nhị thức có thể được áp dụng cho các biến động giá cổ phiếu. Chúng ta chỉ cần xác định hai kết quả có thể xảy ra và xác suất mà mỗi kết quả sẽ xảy ra. Hãy xem xét một cổ phiếu với giá hiện tại là , trong khoảng thời gian tiếp theo, sẽ hoặc tăng giá trị hoặc giảm giá trị (hai kết quả có thể xảy ra duy nhất). Xác suất của một lần tăng giá (xác suất chuyển tiếp tăng, ) là và xác suất của một lần giảm giá (xác suất chuyển tiếp giảm, ) là .
Một cây nhị thức được xây dựng bằng cách hiển thị tất cả các kết hợp có thể của các lần tăng và giảm giá trong một số khoảng thời gian liên tiếp. Đối với hai khoảng thời gian, các kết hợp này là và . Mỗi giá trị có thể dọc theo cây nhị thức là một nút. Hình dưới đây minh họa một cây nhị thức cho ba khoảng thời gian.
Hình: Cây nhị thức
Với giá cổ phiếu ban đầu , , , và , chúng ta có thể tính toán các giá cổ phiếu có thể xảy ra sau hai giai đoạn như sau:
Vì giá cổ phiếu là 50 có thể xảy ra từ cả hai chuyển động hoặc , xác suất của giá cổ phiếu là 50 sau hai giai đoạn (giá trị giữa) là .
Một cây nhị phân với , , và được minh họa trong hình dưới đây. Lưu ý rằng giá trị giữa sau hai giai đoạn (50) bằng với giá trị ban đầu vì , một trường hợp đặc biệt của mô hình nhị phân. Xác suất rằng giá cổ phiếu giảm (<50) sau hai giai đoạn chỉ đơn giản là xác suất của hai chuyển động giảm, .
Hình: Cây nhị phân hai giai đoạn , ,
Một trong những ứng dụng quan trọng của mô hình giá cổ phiếu nhị thức là trong việc định giá quyền chọn. Chúng ta có thể làm cho cây nhị thức cho giá tài sản trở nên thực tế hơn bằng cách rút ngắn độ dài của các giai đoạn và tăng số lượng giai đoạn cũng như các kết quả có thể xảy ra.
H: Định nghĩa phân phối đều liên tục và tính toán, giải thích xác suất, cho một phân phối đều liên tục.
Phân phối đều liên tục được định nghĩa trên một khoảng từ giới hạn dưới, , đến giới hạn trên, , là các tham số của phân phối. Các kết quả chỉ có thể xảy ra giữa và , và vì chúng ta đang xử lý một phân phối liên tục, ngay cả khi , P() = 0. Chính thức, các tính chất của phân phối đều liên tục có thể được mô tả như sau:
- Với tất cả (tức là, với tất cả và giữa các giới hạn và ).
- P( hoặc ) = 0 (tức là xác suất của ngoài các giới hạn là bằng không).
- P() = . Điều này định nghĩa xác suất của các kết quả giữa và .
Đừng bỏ lỡ sự đơn giản của điều này chỉ vì ký hiệu toán học quá phức tạp. Với một phân phối đều liên tục, xác suất của các kết quả trong một khoảng bằng một nửa toàn bộ khoảng là 50%. Xác suất của các kết quả trong một khoảng bằng một phần tư toàn bộ khoảng có thể là 25%.
được phân phối đều trong khoảng từ 2 đến 12. Tính xác suất rằng sẽ nằm trong khoảng từ 4 đến 8.
Câu trả lời:
Hình dưới đây minh họa phân phối đều liên tục này. Lưu ý rằng diện tích bị giới hạn bởi 4 và 8 là 40% tổng xác suất giữa 2 và 12 (là 100%).
Phân phối đều liên tục
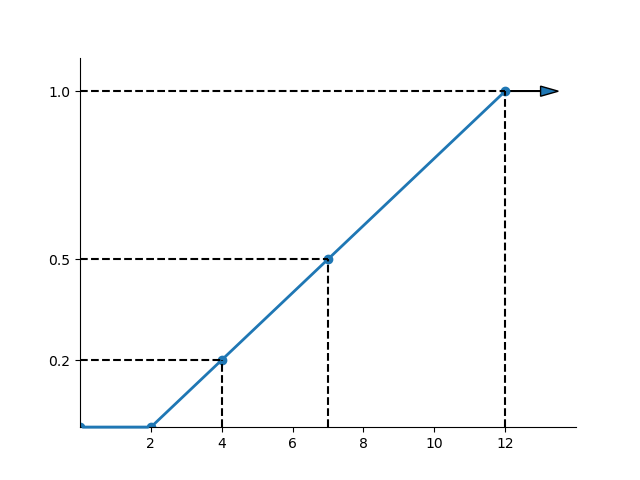
Vì các kết quả là bằng nhau trên các khoảng có kích thước bằng nhau, hàm phân phối tích lũy (cdf) là tuyến tính trên khoảng của biến. Hàm cdf cho phân phối trong ví dụ, xác suất , được hiển thị trong hình sau.
Hình: CDF cho biến phân phối đều liên tục
📝 LUYỆN TẬP
- Điều nào sau đây ít có khả năng là một ví dụ về biến ngẫu nhiên rời rạc?
- A. Số lượng cổ phiếu mà một người sở hữu.
- B. Thời gian mà một nhà quản lý danh mục đầu tư dành cho một khách hàng.
- C. Số ngày mưa trong một tháng ở Iowa City.
- Đối với biến ngẫu nhiên liên tục , xác suất của bất kỳ giá trị đơn lẻ nào của là:
- A. một.
- B. không.
- C. được xác định bởi hàm phân phối tích lũy (cdf).
- Điều nào sau đây ít có khả năng là một phân phối xác suất?
- A. .
- B. .
- C. .
Sử dụng bảng sau để trả lời các câu hỏi từ 4 đến 8.
Phân phối xác suất của một biến ngẫu nhiên rời rạc X
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|---|
| 0.04 | 0.11 | 0.18 | 0.24 | 0.14 | 0.17 | 0.09 | 0.03 |
- Xác suất để là:
- A. 0.18.
- B. 0.24.
- C. 0.43.
- Hàm phân phối tích lũy của 5, hay là:
- A. 0.17.
- B. 0.71.
- C. 0.88.
- Xác suất để lớn hơn 3 là:
- A. 0.24.
- B. 0.43.
- C. 0.67.
- là bao nhiêu?
- A. 0.17.
- B. 0.38.
- C. 0.73.
- Giá trị kỳ vọng của biến ngẫu nhiên là:
- A. 3.35.
- B. 3.70.
- C. 5.47.
- Điều nào sau đây ít có khả năng là điều kiện của một thí nghiệm nhị thức?
- A. Chỉ có hai lần thử.
- B. Các lần thử là độc lập.
- C. Nếu là xác suất thành công, và là xác suất thất bại, thì .
- Điều nào sau đây ít chính xác nhất khi mô tả phân phối nhị thức?
- A. Nó là một phân phối rời rạc.
- B. Xác suất của một kết quả bằng không là không.
- C. Công thức kết hợp được sử dụng trong việc tính xác suất.
- Một nghiên cứu gần đây cho thấy rằng 60% các doanh nghiệp đều có máy fax. Theo bảng phân phối xác suất nhị thức, xác suất có đúng bốn doanh nghiệp có máy fax trong một mẫu ngẫu nhiên gồm sáu doanh nghiệp là:
- A. 0.138.
- B. 0.276.
- C. 0.311.
- Mười phần trăm tất cả các sinh viên tốt nghiệp đại học được tuyển dụng ở lại cùng một công ty hơn năm năm. Trong một mẫu ngẫu nhiên gồm sáu sinh viên tốt nghiệp đại học mới được tuyển dụng, xác suất có đúng hai người ở lại cùng một công ty hơn năm năm gần nhất là:
- A. 0.098.
- B. 0.114.
- C. 0.185.
- Giả sử rằng 40% các ứng viên tham gia kỳ thi đậu ngay lần đầu. Trong một mẫu ngẫu nhiên gồm 15 ứng viên lần đầu tiên tham gia kỳ thi, số ứng viên đậu dự kiến là bao nhiêu?
- A. 0.375.
- B. 4.000.
- C. 6.000.
- Một phân phối đều liên tục có các tham số và . là:
- A. 0.25.
- B. 0.50.
- C. 1.00.
I: Giải thích các đặc tính chính của phân phối chuẩn
Phân phối chuẩn quan trọng vì nhiều lý do. Nhiều biến ngẫu nhiên liên quan đến tài chính và các lĩnh vực chuyên môn khác tuân theo phân phối chuẩn. Trong lĩnh vực đầu tư và quản lý danh mục đầu tư, phân phối chuẩn đóng vai trò trung tâm trong lý thuyết danh mục đầu tư.
Phân phối chuẩn có các đặc tính chính sau:
-
Nó được mô tả hoàn toàn bởi trung bình, , và phương sai, , được biểu diễn là . Nói cách khác, điều này có nghĩa là “X có phân phối chuẩn với trung bình và phương sai .”
-
Độ lệch = 0, có nghĩa là phân phối chuẩn đối xứng quanh trung bình của nó, do đó , và trung bình = trung vị = mode.
-
Hệ số Kurtosis = 3; đây là một thước đo mức độ phẳng của phân phối. Nhớ rằng kurtosis dư được đo tương đối với 3, hệ số kurtosis của phân phối chuẩn.
-
Một tổ hợp tuyến tính của các biến ngẫu nhiên phân phối chuẩn cũng sẽ có phân phối chuẩn.
-
Xác suất của các kết quả xa hơn trên và dưới trung bình ngày càng nhỏ hơn nhưng không về không (các đuôi rất mỏng nhưng kéo dài vô tận).
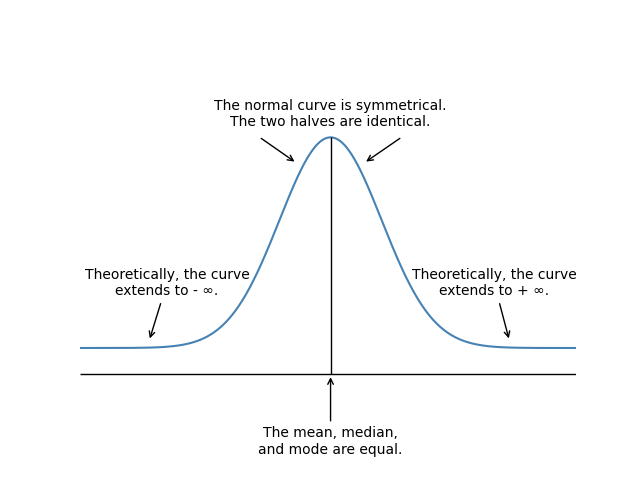
Nhiều đặc tính trong số này có thể được thấy rõ từ việc xem xét đồ thị của hàm mật độ xác suất của phân phối chuẩn như minh họa trong hình dưới.
Hình: Hàm mật độ xác suất của phân phối chuẩn
J: Phân biệt giữa phân phối một biến và phân phối đa biến và giải thích vai trò của tương quan trong phân phối chuẩn đa biến.
Cho đến thời điểm này, chúng ta đã tập trung thảo luận về phân phối một biến (tức là, phân phối của một biến ngẫu nhiên duy nhất). Trong thực tế, các mối quan hệ giữa hai hoặc nhiều biến ngẫu nhiên thường có liên quan. Ví dụ, các nhà đầu tư và các nhà quản lý đầu tư thường quan tâm đến mối quan hệ giữa lợi nhuận của một hoặc nhiều tài sản. Thực tế, như bạn sẽ thấy trong nghiên cứu của mình về các mô hình định giá tài sản và lý thuyết danh mục đầu tư hiện đại, lợi nhuận của một cổ phiếu nhất định và lợi nhuận của S&P 500 hoặc một chỉ số thị trường khác sẽ có ý nghĩa đặc biệt. Bất kể các biến cụ thể là gì, phân tích đồng thời hai hoặc nhiều biến ngẫu nhiên đòi hỏi phải hiểu biết về phân phối đa biến.
Một phân phối đa biến xác định các xác suất liên quan đến một nhóm các biến ngẫu nhiên và chỉ có ý nghĩa khi hành vi của từng biến ngẫu nhiên trong nhóm phụ thuộc một cách nào đó vào hành vi của các biến khác. Cả biến ngẫu nhiên rời rạc và biến ngẫu nhiên liên tục đều có thể có phân phối đa biến. Phân phối đa biến giữa hai biến ngẫu nhiên rời rạc được mô tả bằng các bảng xác suất chung. Đối với các biến ngẫu nhiên liên tục, có thể sử dụng phân phối chuẩn đa biến để mô tả chúng nếu tất cả các biến riêng lẻ đều tuân theo phân phối chuẩn. Như đã đề cập trước đó, một trong những đặc điểm của phân phối chuẩn là một tổ hợp tuyến tính của các biến ngẫu nhiên tuân theo phân phối chuẩn cũng sẽ tuân theo phân phối chuẩn. Ví dụ, nếu lợi nhuận của mỗi cổ phiếu trong một danh mục đầu tư tuân theo phân phối chuẩn, lợi nhuận của danh mục đầu tư cũng sẽ tuân theo phân phối chuẩn.
Vai Trò của Tương Quan trong Phân Phối Chuẩn Đa Biến
Tương tự như phân phối chuẩn một biến, một phân phối chuẩn đa biến có thể được mô tả bằng trung bình và phương sai của các biến ngẫu nhiên riêng lẻ. Ngoài ra, cần phải xác định tương quan giữa các cặp biến riêng lẻ khi mô tả một phân phối đa biến. Tương quan là đặc điểm phân biệt một phân phối đa biến với một phân phối chuẩn một biến. Tương quan chỉ ra sức mạnh của mối quan hệ tuyến tính giữa một cặp biến ngẫu nhiên.
Sử dụng lợi nhuận tài sản làm biến ngẫu nhiên của chúng ta, phân phối chuẩn đa biến cho lợi nhuận trên n tài sản có thể được định nghĩa hoàn chỉnh bằng ba tập hợp tham số sau:
- n giá trị trung bình của n chuỗi lợi nhuận ().
- n phương sai của n chuỗi lợi nhuận ().
- tương quan cặp đôi.
Ví dụ, nếu có hai tài sản, , thì phân phối lợi nhuận đa biến có thể được mô tả bằng hai giá trị trung bình, hai phương sai và một tương quan . Nếu có bốn tài sản, , phân phối đa biến có thể được mô tả bằng bốn giá trị trung bình, bốn phương sai và sáu tương quan . Khi xây dựng một danh mục đầu tư, tất cả các yếu tố khác bằng nhau, sẽ là mong muốn kết hợp các tài sản có tương quan lợi nhuận thấp vì điều này sẽ dẫn đến một danh mục đầu tư có phương sai thấp hơn so với một danh mục đầu tư gồm các tài sản có tương quan cao hơn.
K: Xác định xác suất mà một biến ngẫu nhiên phân phối chuẩn nằm trong một khoảng cho trước.
Một khoảng tin cậy là một phạm vi giá trị xung quanh kết quả kỳ vọng mà trong đó chúng ta mong đợi kết quả thực tế sẽ nằm trong một tỷ lệ phần trăm nhất định. Một khoảng tin cậy 95% là một phạm vi mà chúng ta mong đợi biến ngẫu nhiên sẽ nằm trong đó 95% thời gian. Đối với phân phối chuẩn, khoảng này dựa trên giá trị kỳ vọng (đôi khi được gọi là ước tính điểm) của biến ngẫu nhiên và dựa trên sự biến thiên của nó, mà chúng ta đo lường bằng độ lệch chuẩn.
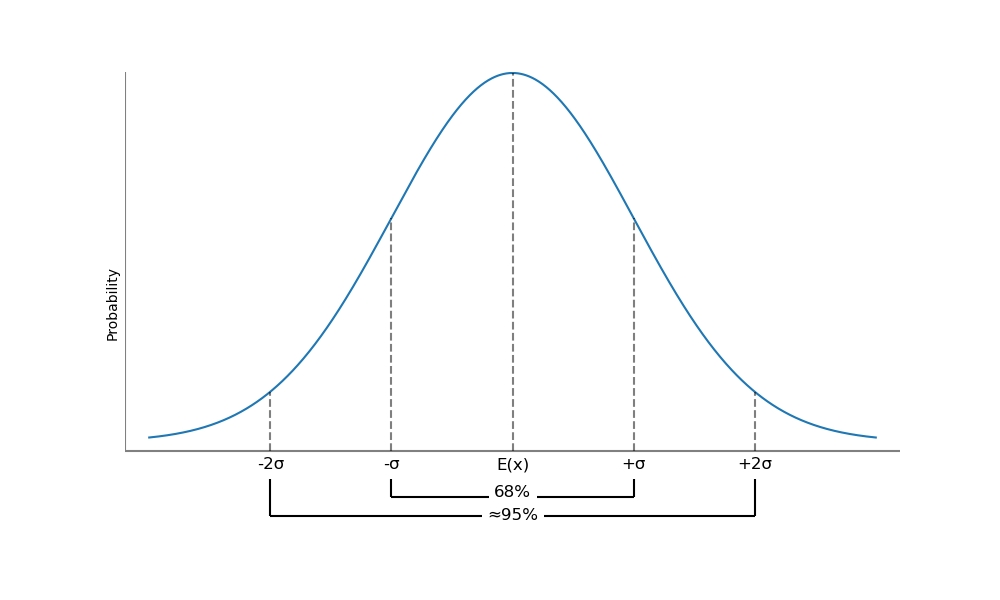
Các khoảng tin cậy cho một phân phối chuẩn được minh họa trong hình sau. Đối với bất kỳ biến ngẫu nhiên phân phối chuẩn nào, 68% kết quả nằm trong một độ lệch chuẩn của giá trị kỳ vọng (trung bình), và khoảng 95% kết quả nằm trong hai độ lệch chuẩn của giá trị kỳ vọng.
Hình: Khoảng Tin Cậy cho một Phân Phối Chuẩn
Trong thực tế, chúng ta sẽ không biết các giá trị thực của trung bình và độ lệch chuẩn của phân phối, mà sẽ ước tính chúng như và . Ba khoảng tin cậy quan trọng nhất là:
- Khoảng tin cậy 90% cho là từ đến .
- Khoảng tin cậy 95% cho là từ đến .
- Khoảng tin cậy 99% cho là từ đến .
Lợi nhuận trung bình của một quỹ tương hỗ là 10.5% mỗi năm và độ lệch chuẩn của lợi nhuận hàng năm là 18%. Nếu lợi nhuận xấp xỉ phân phối chuẩn, khoảng tin cậy 95% cho lợi nhuận của quỹ tương hỗ vào năm sau là bao nhiêu?
Trả lời:
Ở đây và lần lượt là 10.5% và 18%. Vì vậy, khoảng tin cậy 95% cho lợi nhuận, , là:
Một cách tượng trưng, kết quả này có thể được biểu diễn như sau:
Điều này có nghĩa là lợi nhuận hàng năm dự kiến sẽ nằm trong khoảng này 95% thời gian, tức là 95 trên 100 năm.
L: Định nghĩa phân phối chuẩn tắc, giải thích cách chuẩn hóa một biến ngẫu nhiên và tính toán cũng như diễn giải các xác suất sử dụng phân phối chuẩn tắc.
Phân phối chuẩn tắc là một phân phối chuẩn đã được chuẩn hóa để có trung bình bằng không và độ lệch chuẩn bằng 1 [tức là, ]. Để chuẩn hóa một quan sát từ một phân phối chuẩn cho trước, cần tính toán giá trị z của quan sát đó. Giá trị z biểu thị số độ lệch chuẩn mà một quan sát cụ thể lệch so với trung bình của tổng thể. Chuẩn hóa là quá trình chuyển đổi một giá trị quan sát cho một biến ngẫu nhiên thành giá trị z của nó. Công thức sau đây được sử dụng để chuẩn hóa một biến ngẫu nhiên:
Thuật ngữ giá trị z sẽ được sử dụng cho một quan sát chuẩn hóa trong tài liệu này. Các thuật ngữ z-score và z-statistic cũng thường được sử dụng.
Giả sử rằng lợi nhuận hàng năm trên mỗi cổ phần (EPS) của một tổng thể các công ty được phân phối chuẩn với trung bình là $6 và độ lệch chuẩn là $2. Giá trị z cho EPS là $2 và $8 là bao nhiêu?
Trả lời:
Nếu $8, thì z = (x − μ) / σ = ($8 − $6) / $2 = +1
Nếu $2, thì z = (x − μ) / σ = ($2 − $6) / $2 = −2
Ở đây, z = +1 chỉ ra rằng một EPS là $8 cao hơn trung bình một độ lệch chuẩn, và z = −2 có nghĩa là một EPS là $2 thấp hơn trung bình hai độ lệch chuẩn.
Tính Xác Suất Sử Dụng Giá Trị z
Bây giờ chúng ta sẽ chỉ cách sử dụng giá trị chuẩn hóa (giá trị z) và bảng xác suất cho Z để xác định xác suất. Một phần của bảng phân phối tích lũy cho phân phối chuẩn được hiển thị trong hình dưới đây. Chúng ta sẽ gọi bảng này là bảng z, vì nó chứa các giá trị được tạo bằng cách sử dụng hàm mật độ tích lũy cho phân phối chuẩn, được ký hiệu là . Do đó, các giá trị trong bảng z là xác suất quan sát giá trị z nhỏ hơn một giá trị cho trước, [tức là, ]. Các số trong cột đầu tiên là các giá trị z có một chữ số thập phân. Các cột bên phải cung cấp xác suất cho các giá trị z có hai chữ số thập phân.
Lưu ý rằng bảng z trong hình dưới đây chỉ cung cấp xác suất cho các giá trị z dương. Điều này không phải là vấn đề vì chúng ta biết từ tính đối xứng của phân phối chuẩn mà . Các bảng ở phần sau của nhiều sách thực tế cung cấp xác suất cho các giá trị z âm, nhưng chúng ta sẽ chỉ làm việc với phần dương của bảng vì đây có thể là tất cả những gì bạn nhận được trong kỳ thi. Trong hình dưới đây, chúng ta có thể tìm thấy xác suất mà một biến ngẫu nhiên chuẩn sẽ nhỏ hơn 1.66, chẳng hạn. Giá trị trong bảng là 95.15%. Xác suất mà biến ngẫu nhiên sẽ nhỏ hơn -1.66 đơn giản là , đây cũng là xác suất mà biến số sẽ lớn hơn +1.66.
Hình: Xác Suất Tích Lũy Cho Phân Phối Chuẩn
(Xin lưu ý rằng một số hàng đã bị xóa để tiết kiệm không gian.)
| z | .00 | .01 | .02 | .03 | .04 | .05 | .06 | .07 | .08 | .09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | .5000 | .5040 | .5080 | .5120 | .5160 | .5199 | .5239 | .5279 | .5319 | .5359 |
| 0.1 | .5398 | .5438 | .5478 | .5517 | .5557 | .5596 | .5636 | .5675 | .5714 | .5753 |
| 0.2 | .5793 | .5832 | .5871 | .5910 | .5948 | .5987 | .6026 | .6064 | .6103 | .6141 |
| 0.5 | .6915 | |||||||||
| 1.2 | .8849 | .8869 | .8888 | .8907 | .8925 | .8944 | .8962 | .8980 | .8997 | .9015 |
| 1.6 | .9452 | .9463 | .9474 | .9484 | .9495 | .9505 | .9515 | .9525 | .9535 | .9545 |
| 1.8 | .9641 | .9649 | .9656 | .9664 | .9671 | .9678 | .9686 | .9693 | .9699 | .9706 |
| 2.0 | .9772 | .9778 | .9783 | .9788 | .9793 | .9798 | .9803 | .9808 | .9812 | .9817 |
| 2.5 | .9938 | .9940 | .9941 | .9943 | .9945 | .9945 | .9948 | .9949 | .9951 | .9952 |
| 3.0 | .9987 | .9987 | .9987 | .9988 | .9988 | .9989 | .9989 | .9989 | .9989 | .9990 |
- Bảng phân phối chuẩn đầy đủ được bao gồm trong Phụ lục A.
Khi bạn sử dụng xác suất chuẩn, bạn đã xác định vấn đề theo các độ lệch chuẩn so với giá trị trung bình. Hãy xem xét một chứng khoán có lợi tức xấp xỉ chuẩn, lợi tức kỳ vọng là 10% và độ lệch chuẩn của lợi tức là 12%. Xác suất lợi tức lớn hơn 30% được tính dựa trên số độ lệch chuẩn mà 30% cao hơn lợi tức kỳ vọng 10%. 30% cao hơn 20% so với lợi tức kỳ vọng 10%, tức là độ lệch chuẩn cao hơn giá trị trung bình. Chúng ta tra cứu xác suất của lợi tức nhỏ hơn 1.67 độ lệch chuẩn so với giá trị trung bình (0.9525 hoặc 95.25% từ hình trên) và tính xác suất của lợi tức lớn hơn 1.67 độ lệch chuẩn so với giá trị trung bình là .
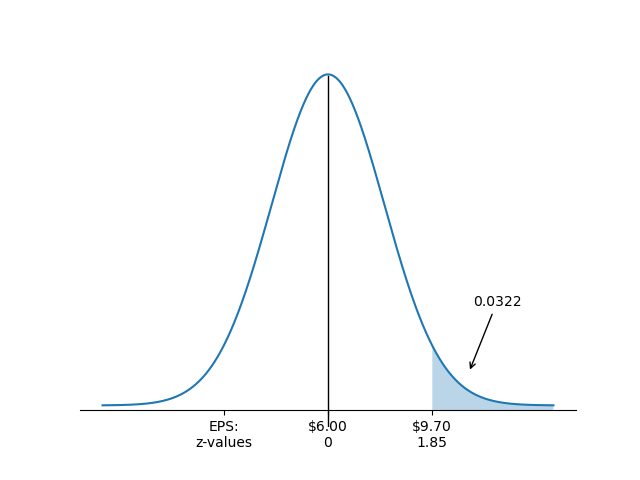
Xét EPS được phân phối với và , xác suất rằng EPS sẽ là hoặc cao hơn là bao nhiêu?
Trả lời:
Ở đây, chúng ta muốn biết , là diện tích dưới đường cong về phía bên phải của giá trị tương ứng với (xem hình dưới đây).
Giá trị cho là:
Tức là, $9.70 nằm cách giá trị trung bình EPS $6 một khoảng 1.85 độ lệch chuẩn.
Từ bảng ta có , nhưng đây là . Chúng ta muốn , tức là .
P(EPS > $9.70)
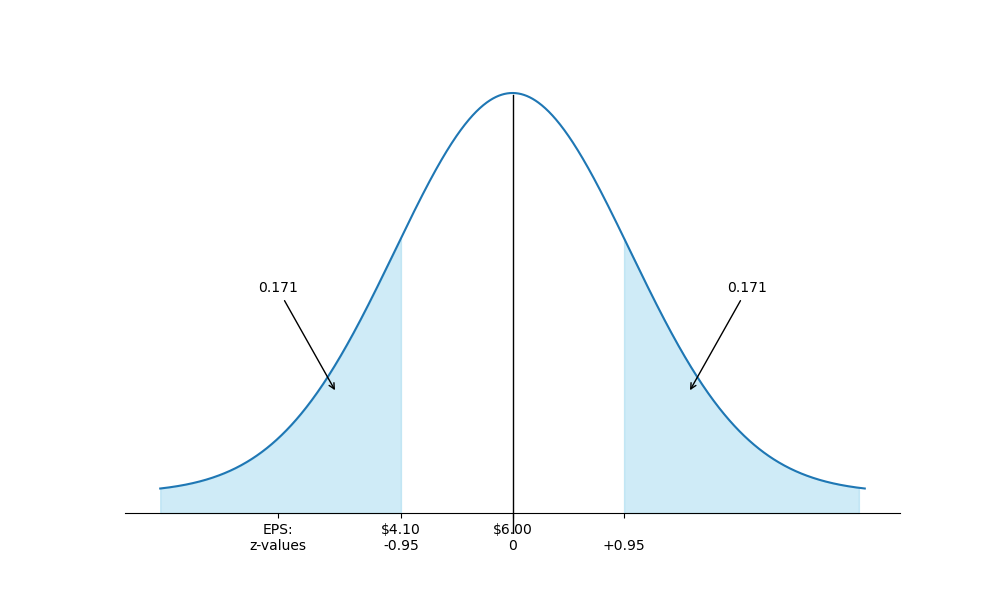
Sử dụng phân phối của EPS với và , phần trăm giá trị EPS quan sát được có khả năng nhỏ hơn là bao nhiêu?
Câu trả lời:
Như được hiển thị trong hình dưới đây, chúng ta muốn biết . Điều này yêu cầu một cách tiếp cận 2 bước giống như ví dụ trước.
vì vậy là độ lệch chuẩn dưới trung bình .
Bây giờ, từ bảng z cho các giá trị âm ở cuối sách này, chúng ta thấy rằng , hoặc .
Tìm xác suất đuôi trái
Bảng z cho chúng ta xác suất rằng kết quả sẽ nhỏ hơn độ lệch chuẩn dưới trung bình.
📝 LUYỆN TẬP
- Một thuộc tính chính của phân phối chuẩn là:
- A. không có độ lệch.
- B. không đối xứng.
- C. không có độ nhọn.
- Tham số nào sau đây cần thiết để mô tả một phân phối chuẩn đa biến?
- A. Beta.
- B. Tương quan.
- C. Bậc tự do.
Sử dụng bảng sau để trả lời Câu hỏi 3.
| z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 |
|---|---|---|---|---|---|
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 |
- Một nghiên cứu về các nhà đầu tư quỹ phòng hộ cho thấy thu nhập hàng năm của họ được phân phối chuẩn với trung bình là $175,000 và độ lệch chuẩn là $25,000. Phần trăm các nhà đầu tư quỹ phòng hộ có thu nhập lớn hơn $150,000 gần nhất với:
- A. 34.13%
- B. 68.26%
- C. 84.13%
- Đối với phân phối chuẩn, giá trị z cho khoảng cách giữa trung bình và một điểm theo:
- A. phương sai.
- B. độ lệch chuẩn.
- C. trung tâm của đường cong.
- Đối với phân phối chuẩn, F(0) là:
- A. 0.0.
- B. 0.1.
- C. 0.5.
3: PHÂN PHỐI LOGNORMAL, MÔ PHỎNG
M: Định nghĩa rủi ro thiếu hụt, tính tỷ lệ an toàn trước và chọn danh mục đầu tư tối ưu bằng cách sử dụng tiêu chí an toàn trước của Roy.
Rủi ro thâm hụt là xác suất rằng giá trị hoặc lợi nhuận của danh mục đầu tư sẽ giảm xuống dưới một giá trị (mục tiêu) cụ thể trong một khoảng thời gian nhất định.
Tiêu chí an toàn đầu tiên của Roy cho rằng danh mục đầu tư tối ưu là danh mục giảm thiểu xác suất rằng lợi nhuận của danh mục sẽ giảm xuống dưới mức chấp nhận tối thiểu. Mức chấp nhận tối thiểu này được gọi là mức ngưỡng. Về mặt ký hiệu, tiêu chí an toàn đầu tiên của Roy có thể được biểu diễn như sau:
trong đó:
- = lợi nhuận danh mục đầu tư
- = lợi nhuận mức ngưỡng
Nếu lợi nhuận danh mục đầu tư phân phối chuẩn, thì tiêu chí an toàn đầu tiên của Roy có thể được biểu diễn như sau:
Lý do đằng sau tiêu chí an toàn đầu tiên được minh họa trong hình sau. Giả sử một nhà đầu tư đang chọn giữa hai danh mục đầu tư: Danh mục A với lợi nhuận kỳ vọng là và độ lệch chuẩn của lợi nhuận là , và Danh mục B với lợi nhuận kỳ vọng là và độ lệch chuẩn của lợi nhuận là . Nhà đầu tư đã tuyên bố rằng anh ta muốn giảm thiểu xác suất mất tiền (lợi nhuận âm). Giả sử rằng lợi nhuận phân phối chuẩn, danh mục đầu tư với lớn hơn sử dụng làm lợi nhuận ngưỡng () sẽ là danh mục có xác suất lợi nhuận âm thấp hơn.
Hình: Tiêu chí an toàn đầu tiên và rủi ro thâm hụt
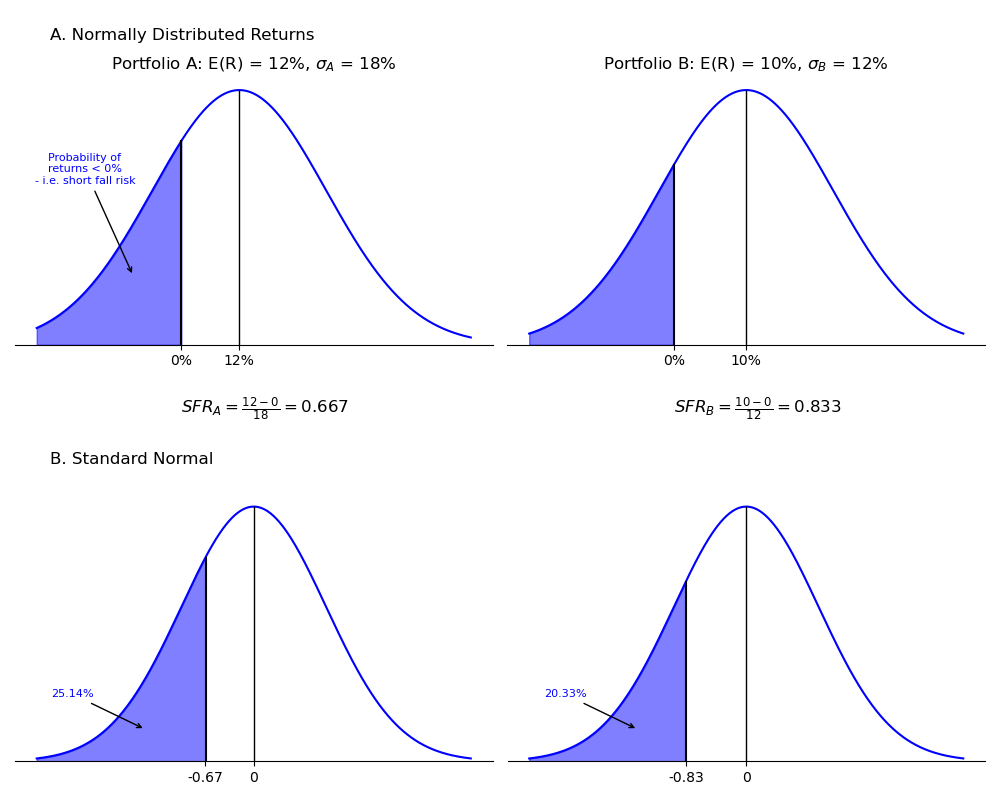
Panel B của hình trên liên quan đến SFRatio với phân phối chuẩn tắc. Lưu ý rằng SFR là số độ lệch chuẩn dưới trung bình. Do đó, danh mục đầu tư với SFR lớn hơn có xác suất thấp hơn về lợi nhuận dưới mức ngưỡng, là lợi nhuận 0% trong ví dụ của chúng ta. Sử dụng bảng z cho các giá trị âm, chúng ta có thể tìm thấy các xác suất ở các đuôi bên trái như đã chỉ ra. Các xác suất này (25% cho Danh mục đầu tư A và 20% cho Danh mục đầu tư B) cũng là rủi ro thiếu hụt cho lợi nhuận mục tiêu 0%, tức là xác suất lợi nhuận âm. Danh mục đầu tư B có SFR cao hơn, có nghĩa là có xác suất lợi nhuận âm thấp hơn.
Tóm lại, khi lựa chọn giữa các danh mục đầu tư có lợi nhuận phân phối chuẩn tắc sử dụng tiêu chí an toàn của Roy, có hai bước:
Bước 1: Tính
Bước 2: Chọn danh mục đầu tư có SFRatio lớn nhất.
Trong năm tới, các nhà quản lý của một quỹ hiến tặng trị giá 120 triệu đô la của một trường cao đẳng đã đặt ra giá trị danh mục đầu tư cuối năm tối thiểu chấp nhận được là 123,6 triệu đô la. Ba danh mục đầu tư đang được xem xét có các lợi nhuận kỳ vọng và độ lệch chuẩn được hiển thị ở hai hàng đầu tiên của bảng sau. Xác định danh mục đầu tư nào là mong muốn nhất sử dụng tiêu chí an toàn của Roy và xác suất giá trị danh mục đầu tư sẽ thấp hơn mục tiêu.
Trả lời:
Lợi nhuận ngưỡng là . Các SFR được hiển thị trong bảng dưới đây. Như đã chỉ ra, lựa chọn tốt nhất là Danh mục đầu tư A vì nó có SFR lớn nhất.
| Tỷ lệ an toàn của Roy | Danh mục đầu tư A | Danh mục đầu tư B | Danh mục đầu tư C |
|---|---|---|---|
| 9% | 11% | 6.6% | |
| 12% | 20% | 8.2% | |
| SFRatio | 0.5 = (9 - 3) / 12 | 0.4 = (11 - 3) / 20 | 0.44 = (6.6 - 3) / 8.2 |
Xác suất giá trị kết thúc của Danh mục đầu tư A thấp hơn 123,6 triệu đô la (lợi nhuận thấp hơn 3%) đơn giản là F(-0.5) mà chúng ta có thể tìm thấy trên bảng z cho các giá trị âm. Xác suất là 0.3085 = 30.85%.
N: Giải thích mối quan hệ giữa phân phối chuẩn và phân phối lognormal và tại sao phân phối lognormal được sử dụng để mô hình hóa giá tài sản.
Phân phối lognormal được tạo ra bởi hàm , trong đó được phân phối chuẩn. Vì logarit tự nhiên, , của là , nên logarit của các biến ngẫu nhiên phân phối lognormal được phân phối chuẩn, do đó có tên gọi như vậy.
Hình dưới đây minh họa sự khác biệt giữa phân phối chuẩn và phân phối lognormal.
Hình: Phân phối Chuẩn vs. Phân phối Lognormal
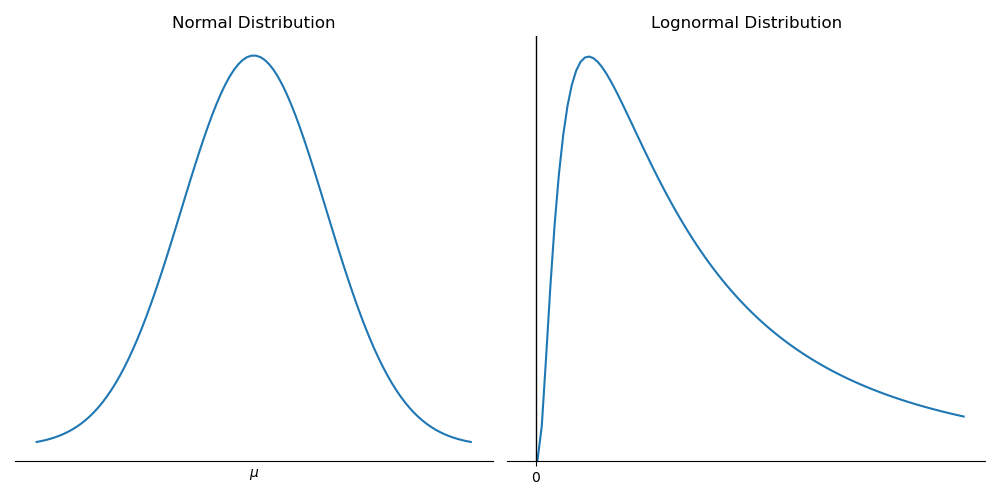
Trong hình trên, chúng ta có thể thấy rằng:
- Phân phối lognormal có độ lệch về phía phải.
- Phân phối lognormal bị giới hạn từ dưới bởi không, vì vậy nó hữu ích để mô hình hóa giá tài sản, vốn không bao giờ có giá trị âm.
Nếu chúng ta sử dụng phân phối chuẩn của lợi nhuận để mô hình hóa giá tài sản theo thời gian, chúng ta sẽ thừa nhận khả năng lợi nhuận nhỏ hơn -100%, điều này sẽ thừa nhận khả năng giá tài sản nhỏ hơn không. Sử dụng phân phối lognormal để mô hình hóa tỷ lệ giá tránh được vấn đề này. Tỷ lệ giá chỉ là giá tài sản cuối kỳ chia cho giá đầu kỳ () và bằng (). Để có được giá tài sản cuối kỳ, chúng ta có thể đơn giản nhân tỷ lệ giá với giá tài sản đầu kỳ. Vì phân phối lognormal có giá trị tối thiểu là không, giá t�ài sản cuối kỳ không thể nhỏ hơn không. Tỷ lệ giá bằng không tương ứng với lợi nhuận kỳ nắm giữ là -100% (tức là giá tài sản đã về không). Nhớ rằng chúng ta đã sử dụng tỷ lệ giá làm các hệ số tăng và giảm (bội số) trong việc xây dựng cây nhị phân cho các biến động giá cổ phiếu qua một số kỳ.
O: Phân biệt giữa lãi suất gộp rời rạc và liên tục và tính toán và diễn giải lãi suất gộp liên tục, cho một tỷ suất lợi nhuận giữ trong một thời kỳ nhất định.
Lãi suất gộp rời rạc là lãi suất gộp chúng ta quen thuộc, được xác định với một kỳ gộp rời rạc, như nửa năm hoặc hàng quý. Nhớ rằng tần suất gộp càng cao thì lãi suất hàng năm hiệu quả càng lớn. Với lãi suất công bố là 10%, gộp nửa năm cho kết quả là:
và gộp hàng tháng cho kết quả là:
Gộp hàng ngày hoặc thậm chí hàng giờ sẽ cho lãi suất hiệu quả lớn hơn nữa. Giới hạn của bài toán này, khi các kỳ gộp trở nên ngắn hơn và ngắn hơn, được gọi là gộp liên tục. Lãi suất hàng năm hiệu quả, dựa trên gộp liên tục cho một lãi suất hàng năm công bố là , có thể tính từ công thức:
Dựa trên lãi suất công bố là 10%, lãi suất hiệu quả với gộp liên tục là . Hãy kiểm chứng điều này bằng cách nhập 0.1 vào máy tính của bạn và tìm chức năng .
Vì logarit tự nhiên, , của là , chúng ta có thể lấy lãi suất gộp liên tục từ lãi suất hàng năm hiệu quả bằng cách sử dụng chức năng của máy tính. Sử dụng ví dụ trước đó, . Kiểm chứng điều này bằng cách nhập 1.105171 vào máy tính của bạn và sau đó nhập phím . (Sử dụng máy tính HP, các phím là 1.105171 [g] [ln].)
Chúng ta có thể sử dụng phương pháp này để tìm lãi suất gộp liên tục sẽ tạo ra một tỷ suất lợi nhuận giữ trong một thời kỳ nhất định. Nếu chúng ta có một tỷ suất lợi nhuận giữ trong một năm là 12.5%, lãi suất gộp liên tục tương đương là . Vì tính toán dựa trên 1 cộng với tỷ suất lợi nhuận giữ, chúng ta cũng có thể làm tính toán trực tiếp từ tỷ lệ giá. Tỷ lệ giá chỉ là giá trị cuối kỳ chia cho giá trị đầu kỳ. Lãi suất gộp liên tục là:
Một cổ phiếu được mua với giá $100 và bán một năm sau với giá $120. Tính tỷ suất lợi nhuận hàng năm của nhà đầu tư theo cách gộp liên tục.
Trả lời:
Nếu chúng ta được cung cấp lợi nhuận (20%) thay vì, tính toán là:
Một tính chất của lãi suất gộp liên tục là chúng có thể cộng dồn cho nhiều kỳ. Lưu ý rằng tỷ suất lợi nhuận (hiệu quả) trong kỳ giữ hai năm được tính bằng cách nhân đôi lãi suất gộp hàng năm. Nếu , tỷ suất lợi nhuận (hiệu quả) trong kỳ giữ hai năm là . Nói chung, tỷ suất lợi nhuận sau năm, khi lãi suất gộp hàng năm là , được tính bằng:
Dựa trên kết quả đầu tư trong một giai đoạn 2 năm, chúng ta có thể tính lãi suất gộp liên tục 2 năm và chia cho hai để có lãi suất hàng năm. Xem xét một khoản đầu tư tăng từ $1,000 lên $1,221.40 trong giai đoạn 2 năm. Lãi suất gộp liên tục 2 năm là , và lãi suất gộp hàng năm () là .
P: Giải thích mô phỏng Monte Carlo và mô tả các ứng dụng và hạn chế của nó.
Mô phỏng Monte Carlo là một kỹ thuật dựa trên việc tạo ra lặp đi lặp lại một hoặc nhiều yếu tố rủi ro ảnh hưởng đến giá trị chứng khoán, nhằm tạo ra một phân phối các giá trị chứng khoán. Đối với mỗi yếu tố rủi ro, nhà phân tích phải chỉ định các thông số của phân phối xác suất mà yếu tố rủi ro được giả định tuân theo. Sau đó, một máy tính được sử dụng để tạo ra các giá trị ngẫu nhiên cho mỗi yếu tố rủi ro dựa trên các phân phối xác suất giả định của nó. Mỗi tập hợp các yếu tố rủi ro được tạo ngẫu nhiên được sử dụng với mô hình định giá để định giá chứng khoán. Quy trình này được lặp lại nhiều lần (hàng trăm, hàng ngàn, hoặc hàng chục ngàn lần), và phân phối các giá trị tài sản mô phỏng được sử dụng để rút ra các suy luận về giá trị kỳ vọng (trung bình) của chứng khoán và có thể là phương sai của các giá trị chứng khoán xung quanh trung bình nữa.
Ví dụ, hãy xem xét việc định giá quyền chọn cổ phiếu chỉ có thể được thực hiện vào một ngày cụ thể. Yếu tố rủi ro chính là giá trị của chính cổ phiếu đó, nhưng lãi suất cũng có thể ảnh hưởng đến việc định giá. Quy trình mô phỏng sẽ là:
- Chỉ định các phân phối xác suất của giá cổ phiếu và lãi suất liên quan, cũng như các thông số (trung bình, phương sai, có thể là độ lệch) của các phân phối này.
- Tạo ngẫu nhiên các giá trị cho cả giá cổ phiếu và lãi suất.
- Định giá các quyền chọn cho mỗi cặp giá trị yếu tố rủi ro.
- Sau nhiều lần lặp lại, tính giá trị trung bình của quyền chọn và sử dụng nó như là ước tính của bạn về giá trị của quyền chọn.
Mô phỏng Monte Carlo được sử dụng để:
- Định giá các chứng khoán phức tạp.
- Mô phỏng lãi/lỗ từ một chiến lược giao dịch.
- Tính toán ước lượng giá trị rủi ro (VaR) để xác định mức độ rủi ro của một danh mục tài sản và nợ phải trả.
- Mô phỏng tài sản và nợ phải trả của quỹ hưu trí theo thời gian để kiểm tra sự biến động của sự khác biệt giữa hai yếu tố này.
- Định giá các danh mục tài sản có phân phối lợi nhuận không chuẩn.
Hạn chế của mô phỏng Monte Carlo là nó khá phức tạp và sẽ cung cấp các câu trả lời không tốt hơn các giả định về các phân phối của các yếu tố rủi ro và mô hình định giá/đánh giá được sử dụng. Ngoài ra, mô phỏng không phải là một phương pháp phân tích, mà là một phương pháp thống kê, và không thể cung cấp những hiểu biết sâu sắc mà các phương pháp phân tích có thể.
Q: So sánh mô phỏng Monte Carlo và mô phỏng lịch sử.
Mô phỏng lịch sử dựa trên những thay đổi thực tế về giá trị hoặc những thay đổi thực tế trong các yếu tố rủi ro qua một giai đoạn trước đó. Thay vì mô hình hóa phân phối các yếu tố rủi ro, như trong mô phỏng Monte Carlo, tập hợp tất cả các thay đổi trong các yếu tố rủi ro liên quan qua một giai đoạn trước đó được sử dụng. Mỗi lần lặp lại của mô phỏng bao gồm việc chọn ngẫu nhiên một trong những thay đổi trước đó cho mỗi yếu tố rủi ro và tính toán giá trị của tài sản hoặc danh mục đầu tư dựa trên những thay đổi trong các yếu tố rủi ro đó.
Mô phỏng lịch sử có lợi thế là sử dụng phân phối thực tế của các yếu tố rủi ro do đó phân phối các thay đổi trong các yếu tố rủi ro không cần phải ước tính. Nó gặp phải vấn đề là những thay đổi trong quá khứ của các yếu tố rủi ro có thể không phải là chỉ dẫn tốt cho những thay đổi trong tương lai. Các sự kiện xảy ra không thường xuyên có thể không được phản ánh trong kết quả mô phỏng lịch sử trừ khi các sự kiện đó đã xảy ra trong giai đoạn mà từ đó các giá trị cho các yếu tố rủi ro được lấy. Một hạn chế bổ sung của mô phỏng lịch sử là nó không thể giải quyết các câu hỏi kiểu “điều gì sẽ xảy ra nếu” mà mô phỏng Monte Carlo có thể. Với mô phỏng Monte Carlo, chúng ta có thể điều tra tác động lên phân phối giá trị chứng khoán/danh mục đầu tư nếu chúng ta tăng phương sai của một trong các yếu tố rủi ro lên 20%; với mô phỏng lịch sử chúng ta không thể làm điều này.
📝 LUYỆN TẬP
Sử dụng bảng sau để trả lời Câu hỏi 1 và 2.
| Danh mục đầu tư | Danh mục A | Danh mục B | Danh mục C |
|---|---|---|---|
| 5% | 11% | 18% | |
| 8% | 21% | 40% |
- Với mức ngưỡng lợi nhuận là 4%, sử dụng tiêu chí an toàn của Roy để chọn danh mục đầu tư tối ưu. Danh mục:
- A. A.
- B. B.
- C. C.
- Với mức ngưỡng lợi nhuận là 0%, sử dụng tiêu chí an toàn của Roy để chọn danh mục đầu tư tối ưu. Danh mục:
- A. A.
- B. B.
- C. C.
- Danh mục A có tỷ lệ an toàn là 1.3 với mức ngưỡng lợi nhuận là 2%. Rủi ro thiếu hụt cho mức ngưỡng lợi nhuận là 2% là bao nhiêu?
- A. 9.68%.
- B. 40.30%.
- C. 90.30%.
- Đối với phân phối lognormal:
- A. giá trị trung bình bằng giá trị trung vị.
- B. xác suất của một kết quả âm là bằng không.
- C. xác suất của một kết quả dương là 50%.
- Nếu giá ban đầu của một cổ phiếu là 20 đô la và giá cuối năm của nó là 23 đô la, thì tỷ suất lợi nhuận hàng năm liên tục của nó là:
- A. 13.64%.
- B. 13.98%.
- C. 15.00%.
- Một cổ phiếu đã tăng gấp đôi giá trị trong năm ngoái. Tỷ suất lợi nhuận liên tục của nó trong giai đoạn đó gần nhất với:
- A. 18.2%.
- B. 69.3%.
- C. 100.0%.
- Sử dụng các giá trị tham số giả định và trình tạo số ngẫu nhiên để nghiên cứu hành vi của một số loại tài sản là một phần của:
- A. phân tích lịch sử.
- B. mô phỏng Monte Carlo.
- C. chuẩn hóa một biến ngẫu nhiên.