Lấy mẫu và Ước lượng

Chủ đề này bao gồm các mẫu ngẫu nhiên và suy luận về các giá trị trung bình của dân số từ dữ liệu mẫu. Điều quan trọng là bạn phải biết định lý giới hạn trung tâm, vì nó cho phép chúng ta sử dụng thống kê mẫu để xây dựng các khoảng tin cậy cho ước lượng điểm của giá trị trung bình dân số. Đảm bảo rằng bạn có thể tính toán các khoảng tin cậy cho giá trị trung bình dân số dựa trên các ước lượng tham số mẫu và mức ý nghĩa, và biết khi nào nên sử dụng thống kê $z$ so với thống kê $t$. Bạn cũng nên hiểu các thủ tục cơ bản để tạo mẫu ngẫu nhiên và nhận ra các dấu hiệu cảnh báo của các sai lệch mẫu khác nhau từ các mẫu không ngẫu nhiên.

1: ĐỊNH LÝ GIỚI HẠN TRUNG TÂM VÀ SAI SỐ CHUẨN

Trong nhiều ứng dụng thống kê thực tế, việc nghiên cứu toàn bộ dân số là không khả thi (hoặc không thể). Khi điều này xảy ra, một nhóm con của dân số, được gọi là mẫu, có thể được đánh giá. Dựa trên mẫu này, các tham số của dân số cơ bản có thể được ước lượng.

Ví dụ, thay vì cố gắng đo lường hiệu suất của thị trường chứng khoán Mỹ bằng cách quan sát hiệu suất của tất cả khoảng 10.000 cổ phiếu giao dịch ở Hoa Kỳ tại bất kỳ thời điểm nào, có thể đo lường hiệu suất của nhóm con 500 cổ phiếu trong S&P 500. Kết quả phân tích thống kê của mẫu này sau đó có thể được sử dụng để rút ra kết luận về toàn bộ dân số cổ phiếu của Mỹ.

A: Định nghĩa lấy mẫu ngẫu nhiên đơn giản và phân phối mẫu.

B: Giải thích sai số lấy mẫu.

Lấy mẫu ngẫu nhiên đơn giản là phương pháp chọn một mẫu sao cho mỗi mục hoặc người trong tổng thể đang được nghiên cứu có cùng xác suất được bao gồm trong mẫu. Ví dụ về lấy mẫu ngẫu nhiên đơn giản, giả sử bạn muốn chọn một mẫu gồm năm mục từ một nhóm gồm 50 mục. Điều này có thể được thực hiện bằng cách đánh số từng mục trong 50 mục, đặt chúng vào một cái mũ và lắc mũ. Sau đó, có thể rút ngẫu nhiên một số từ cái mũ. Lặp lại quá trình này (thí nghiệm) bốn lần nữa sẽ tạo ra một tập hợp năm số. Năm số được rút ra (mục) sẽ tạo thành một mẫu ngẫu nhiên đơn giản từ tổng thể. Trong các ứng dụng như thế này, một bảng số ngẫu nhiên hoặc một trình tạo số ngẫu nhiên từ máy tính thường được sử dụng để tạo mẫu. Một cách khác để tạo ra một mẫu ngẫu nhiên gần đúng là lấy mẫu hệ thống, chọn mỗi thành viên thứ n từ tổng thể. Sai số lấy mẫu là sự khác biệt giữa thống kê mẫu (trung bình, phương sai hoặc độ lệch chuẩn của mẫu) và tham số tổng thể tương ứng của nó (trung bình thực, phương sai hoặc độ lệch chuẩn của tổng thể). Ví dụ, sai số lấy mẫu cho trung bình như sau:

$$\text{sampling error of the mean} = \text{sample mean} - \text{population mean} = \bar{x} - \mu$$

Phân phối mẫu

Điều quan trọng là phải nhận ra rằng thống kê mẫu tự nó là một biến ngẫu nhiên và do đó, có một phân phối xác suất. Phân phối mẫu của thống kê mẫu là phân phối xác suất của tất cả các thống kê mẫu có thể tính được từ một tập hợp các mẫu có cùng kích thước được rút ngẫu nhiên từ cùng một tổng thể. Hãy nghĩ về nó như phân phối xác suất của một thống kê từ nhiều mẫu.

Ví dụ, giả sử một mẫu ngẫu nhiên gồm 100 trái phiếu được chọn từ một tổng thể của một chỉ số trái phiếu đô thị chính gồm 1.000 trái phiếu, sau đó tính toán trung bình lợi nhuận của mẫu 100 trái phiếu. Lặp lại quá trình này nhiều lần sẽ dẫn đến nhiều ước tính khác nhau về trung bình lợi nhuận của tổng thể (tức là, một cho mỗi mẫu). Phân phối của những ước tính này của trung bình là phân phối mẫu của trung bình.

Điều quan trọng cần lưu ý là phân phối mẫu này khác biệt với phân phối của giá thực tế của 1.000 trái phiếu trong tổng thể cơ bản và sẽ có các tham số khác nhau.

C: Phân biệt giữa lấy mẫu ngẫu nhiên đơn giản và lấy mẫu ngẫu nhiên phân tầng.

Lấy mẫu ngẫu nhiên phân tầng sử dụng một hệ thống phân loại để tách tổng thể thành các nhóm nhỏ hơn dựa trên một hoặc nhiều đặc điểm phân biệt. Từ mỗi nhóm phụ, hoặc tầng, một mẫu ngẫu nhiên được lấy và kết quả được gộp lại. Kích thước của các mẫu từ mỗi tầng dựa trên kích thước của tầng đó so với tổng thể.

Lấy mẫu phân tầng thường được sử dụng trong lập chỉ mục trái phiếu vì sự khó khăn và chi phí của việc tái tạo hoàn toàn tổng thể trái phiếu. Trong trường hợp này, trái phiếu trong một tổng thể được phân loại (phân tầng) theo các yếu tố rủi ro trái phiếu chính như thời hạn, kỳ hạn, tỷ lệ coupon, và các yếu tố tương tự. Sau đó, các mẫu được rút từ mỗi danh mục riêng biệt và kết hợp để tạo thành mẫu cuối cùng.

Để thấy cách hoạt động của nó, giả sử bạn muốn xây dựng một danh mục trái phiếu được lập chỉ mục theo chỉ số trái phiếu đô thị chính bằng cách sử dụng phương pháp lấy mẫu ngẫu nhiên phân tầng. Đầu tiên, toàn bộ tổng thể của 1.000 trái phiếu đô thị trong chỉ số có thể được phân loại dựa trên kỳ hạn và tỷ lệ coupon. Sau đó, các ô (tầng) có thể được tạo ra cho các kết hợp kỳ hạn/tỷ lệ coupon khác nhau, và các mẫu ngẫu nhiên được rút từ mỗi ô kỳ hạn/tỷ lệ coupon. Để lấy mẫu từ một ô chứa 50 trái phiếu có kỳ hạn từ 2 đến 4 năm và tỷ lệ coupon dưới 5%, chúng tôi sẽ chọn năm trái phiếu. Số lượng trái phiếu được rút ra từ một ô nhất định tương ứng với trọng lượng của ô đó so với tổng thể (chỉ số), hoặc (50 / 1000) x (100) = 5 trái phiếu. Quá trình này được lặp lại cho tất cả các ô kỳ hạn/tỷ lệ coupon, và các mẫu cá nhân được kết hợp để tạo thành danh mục.

Bằng cách sử dụng phương pháp lấy mẫu phân tầng, chúng ta đảm bảo rằng chúng ta lấy mẫu năm trái phiếu từ ô này. Nếu chúng ta sử dụng phương pháp lấy mẫu ngẫu nhiên đơn giản, sẽ không có gì đảm bảo rằng chúng ta sẽ lấy mẫu bất kỳ trái phiếu nào trong ô này. Hoặc, chúng ta có thể đã chọn nhiều hơn năm trái phiếu từ ô này.

D: Phân biệt giữa dữ liệu chuỗi thời gian và dữ liệu chéo.

Dữ liệu chuỗi thời gian bao gồm các quan sát được lấy trong một khoảng thời gian tại các khoảng thời gian cụ thể và cách đều nhau. Tập hợp lợi nhuận hàng tháng của cổ phiếu Microsoft từ tháng 1 năm 1994 đến tháng 1 năm 2004 là một ví dụ về mẫu dữ liệu chuỗi thời gian.

Dữ liệu chéo là một mẫu các quan sát được lấy tại một thời điểm duy nhất. Mẫu lợi nhuận trên mỗi cổ phiếu đã báo cáo của tất cả các công ty Nasdaq tính đến ngày 31 tháng 12 năm 2004 là một ví dụ về mẫu dữ liệu chéo.

Dữ liệu chuỗi thời gian và dữ liệu chéo có thể được kết hợp trong cùng một tập dữ liệu. Dữ liệu dọc là các quan sát theo thời gian của nhiều đặc điểm của cùng một thực thể, chẳng hạn như tỷ lệ thất nghiệp, lạm phát và tốc độ tăng trưởng GDP của một quốc gia trong 10 năm. Dữ liệu bảng chứa các quan sát theo thời gian của cùng một đặc điểm đối với nhiều thực thể, chẳng hạn như tỷ lệ nợ trên vốn chủ sở hữu của 20 công ty trong 24 quý gần nhất. Dữ liệu bảng và dữ liệu dọc thường được trình bày dưới dạng bảng hoặc bảng tính.

E: Giải thích định lý giới hạn trung tâm và tầm quan trọng của nó.

Định lý giới hạn trung tâm phát biểu rằng đối với các mẫu ngẫu nhiên đơn giản có kích thước n từ một quần thể có trung bình $μ$ và phương sai hữu hạn $\sigma^2$, phân phối mẫu của trung bình mẫu $\bar{x}$ tiến tới một phân phối xác suất chuẩn với trung bình μ và phương sai bằng $\frac{\sigma^2}{n}$ khi kích thước mẫu trở nên lớn.

Định lý giới hạn trung tâm cực kỳ hữu ích vì phân phối chuẩn tương đối dễ áp dụng cho việc kiểm định giả thuyết và xây dựng khoảng tin cậy. Các suy luận cụ thể về trung bình của quần thể có thể được đưa ra từ trung bình mẫu, bất kể phân phối của quần thể, miễn là kích thước mẫu “đủ lớn,” thường có nghĩa là n ≥ 30.

Các thuộc tính quan trọng của định lý giới hạn trung tâm bao gồm:

• Nếu kích thước mẫu n đủ lớn (n ≥ 30), phân phối mẫu của trung bình mẫu sẽ xấp xỉ chuẩn. Hãy nhớ rằng, các mẫu ngẫu nhiên có kích thước n liên tục được lấy từ một quần thể lớn hơn. Mỗi mẫu ngẫu nhiên này có trung bình riêng của nó, mà bản thân nó là một biến ngẫu nhiên, và tập hợp các trung bình mẫu này có một phân phối xấp xỉ chuẩn.
• Trung bình của quần thể, μ, và trung bình của phân phối của tất cả các trung bình mẫu có thể có bằng nhau.
• Phương sai của phân phối trung bình mẫu là $\frac{\sigma^2}{n}$, phương sai của quần thể chia cho kích thước mẫu.

F: Tính toán và diễn giải sai số chuẩn của trung bình mẫu.

Sai số chuẩn của trung bình mẫu là độ lệch chuẩn của phân phối các trung bình mẫu.

Khi độ lệch chuẩn của tổng thể, $\sigma$, được biết, sai số chuẩn của trung bình mẫu được tính như sau:

$$\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}}$$

trong đó:

• $\sigma_{\bar{x}}$ = sai số chuẩn của trung bình mẫu
• $\sigma$ = độ lệch chuẩn của tổng thể
• $n$ = kích thước mẫu

VÍ DỤ: Sai số chuẩn của trung bình mẫu (độ lệch chuẩn tổng thể đã biết)

Mức lương theo giờ trung bình của công nhân nông trại Iowa là $13,50 với độ lệch chuẩn của tổng thể là $2,90. Tính toán và diễn giải sai số chuẩn của trung bình mẫu với kích thước mẫu là 30.

Trả lời:

Vì độ lệch chuẩn của tổng thể, $\sigma$, được biết, sai số chuẩn của trung bình mẫu được biểu thị như sau:

$$\sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}} = \frac{2.90}{\sqrt{30}} = \$0.53$$

Điều này có nghĩa là nếu chúng ta lấy nhiều mẫu kích thước 30 từ dân số công nhân nông trại Iowa và tạo ra phân phối mẫu của các trung bình mẫu, chúng ta sẽ có một phân phối với trung bình dự kiến là $13,50 và sai số chuẩn (độ lệch chuẩn của các trung bình mẫu) là $0.53.

Trên thực tế, độ lệch chuẩn của tổng thể hầu như không bao giờ được biết. Thay vào đó, sai số chuẩn của trung bình mẫu phải được ước tính bằng cách chia độ lệch chuẩn của mẫu cho $\sqrt{n}$:

$$s_{\bar{x}} = \frac{s}{\sqrt{n}}$$

VÍ DỤ: Sai số chuẩn của trung bình mẫu (độ lệch chuẩn tổng thể chưa biết)

Giả sử một mẫu chứa 30 mức lợi nhuận hàng tháng gần đây của McCreary, Inc. Trung bình lợi nhuận là 2% và độ lệch chuẩn của mẫu là 20%. Tính toán và diễn giải sai số chuẩn của trung bình mẫu.

Trả lời:

Vì $\sigma$ chưa được biết, sai số chuẩn của trung bình mẫu là:

$$s_{\bar{x}} = \frac{s}{\sqrt{n}} = \frac{20\%}{\sqrt{30}} = 3.6\%$$

Điều này có nghĩa là nếu chúng ta lấy tất cả các mẫu có kích thước 30 từ các mức lợi nhuận hàng tháng của McCreary và tạo ra phân phối mẫu của các trung bình mẫu, trung bình sẽ là 2% với sai số chuẩn là 3.6%.

VÍ DỤ: Sai số chuẩn của trung bình mẫu (phương sai tổng thể không xác định)

Tiếp tục với ví dụ của chúng ta, giả sử rằng thay vì kích thước mẫu là 30, chúng ta lấy mẫu của 200 lợi nhuận hàng tháng trước đây của McCreary, Inc. Để làm nổi bật ảnh hưởng của kích thước mẫu đến sai số chuẩn mẫu, hãy giả định rằng lợi nhuận trung bình và độ lệch chuẩn của mẫu lớn hơn này vẫn là 2% và 20%. Bây giờ, tính sai số chuẩn của trung bình mẫu cho mẫu 200 lợi nhuận.

Câu trả lời:

Sai số chuẩn của trung bình mẫu được tính như sau:

$$s_{\bar{x}} = \frac{s}{\sqrt{n}} = \frac{20\%}{\sqrt{200}} = 1.4\%$$

Kết quả của hai ví dụ trước minh họa một thuộc tính quan trọng của các phân phối mẫu. Lưu ý rằng giá trị của sai số chuẩn của trung bình mẫu giảm từ 3.6% xuống 1.4% khi kích thước mẫu tăng từ 30 lên 200. Điều này là do khi kích thước mẫu tăng lên, trung bình mẫu gần hơn, trung bình, đến trung bình thực của tổng thể. Nói cách khác, phân phối của các trung bình mẫu quanh trung bình tổng thể ngày càng nhỏ hơn, do đó sai số chuẩn của trung bình mẫu giảm.

LƯU Ý CỦA GIÁO SƯ

Tôi nhận được rất nhiều câu hỏi về việc khi nào sử dụng $\sigma$ và $\sigma / \sqrt{n}$. Chỉ cần nhớ rằng độ lệch chuẩn của các trung bình của nhiều mẫu nhỏ hơn độ lệch chuẩn của các quan sát đơn lẻ. Nếu độ lệch chuẩn của lợi nhuận cổ phiếu hàng tháng là 2%, thì sai số chuẩn (độ lệch chuẩn) của lợi nhuận trung bình hàng tháng trong sáu tháng tới là $2\% / \sqrt{6} = 0.82\%$. Trung bình của một số quan sát của một biến ngẫu nhiên sẽ ít phân tán hơn (có độ lệch chuẩn thấp hơn) xung quanh giá trị kỳ vọng so với một quan sát đơn lẻ của biến ngẫu nhiên đó.

G: Xác định và mô tả các thuộc tính mong muốn của một ước lượng.

Bất kể chúng ta quan tâm đến ước lượng điểm hay khoảng tin cậy, có một số thuộc tính thống kê làm cho một số ước lượng trở nên mong muốn hơn những ước lượng khác. Các thuộc tính mong muốn của một ước lượng là không chệch, hiệu quả và nhất quán.

• Một ước lượng không chệch là ước lượng mà giá trị kỳ vọng của nó bằng với tham số mà bạn đang cố gắng ước lượng. Ví dụ, vì giá trị kỳ vọng của trung bình mẫu bằng với trung bình tổng thể $\mathbb{E}(\bar{x}) = \mu$, trung bình mẫu là một ước lượng không chệch của trung bình tổng thể.
• Một ước lượng không chệch cũng hiệu quả nếu phương sai của phân phối mẫu của nó nhỏ hơn tất cả các ước lượng không chệch khác của tham số mà bạn đang cố gắng ước lượng. Ví dụ, trung bình mẫu là một ước lượng không chệch và hiệu quả của trung bình tổng thể.
• Một ước lượng nhất quán là ước lượng mà độ chính xác của ước lượng tham số tăng lên khi kích thước mẫu tăng lên. Khi kích thước mẫu tăng, sai số chuẩn của trung bình mẫu giảm và phân phối mẫu gần hơn với trung bình tổng thể. Thực tế, khi kích thước mẫu tiến tới vô hạn, sai số chuẩn tiến tới không.

📝 LUYỆN TẬP

1. Một mẫu ngẫu nhiên đơn giản là một mẫu được rút ra theo cách mà mỗi thành viên của quần thể có:

• A. một số cơ hội được chọn vào mẫu.
• B. cơ hội bằng nhau để được bao gồm trong mẫu.
• C. cơ hội 1% để được bao gồm trong mẫu.

2. Phân phối mẫu của một thống kê là phân phối xác suất tạo thành từ tất cả các:

• A. quan sát từ quần thể cơ bản.
• B. thống kê mẫu được tính từ các mẫu có kích thước khác nhau được rút ra từ cùng một quần thể.
• C. thống kê mẫu được tính từ các mẫu có cùng kích thước được rút ra từ cùng một quần thể.

3. Sai số lấy mẫu được định nghĩa là:

• A. lỗi xảy ra khi rút ra một mẫu có ít hơn 30 phần tử.
• B. lỗi xảy ra trong quá trình thu thập, ghi chép và lập bảng dữ liệu.
• C. sự khác biệt giữa giá trị của một thống kê mẫu và giá trị của tham số quần thể tương ứng.

4. Tuổi trung bình của tất cả các ứng viên CFA là 28 năm. Tuổi trung bình của một mẫu ngẫu nhiên gồm 100 ứng viên được tìm thấy là 26.5 năm. Sự khác biệt 1.5 năm này được gọi là:

• A. lỗi ngẫu nhiên.
• B. sai số lấy mẫu.
• C. lỗi quần thể.

5. Mẫu tỷ lệ nợ/vốn chủ sở hữu của 25 ngân hàng niêm yết công khai tại Hoa Kỳ tính đến cuối năm tài chính 2003 là một ví dụ của:

• A. ước tính điểm.
• B. dữ liệu cắt ngang.
• C. mẫu ngẫu nhiên phân tầng.

6. Để áp dụng định lý giới hạn trung tâm cho phân phối mẫu của trung bình mẫu, mẫu thường được coi là lớn nếu $n$ lớn hơn:

• A. 20.
• B. 25.
• C. 30.

7. Nếu $n$ lớn và độ lệch chuẩn của quần thể không biết, sai số chuẩn của phân phối mẫu của trung bình mẫu bằng:

• A. độ lệch chuẩn mẫu chia cho kích thước mẫu.
• B. độ lệch chuẩn quần thể nhân với kích thước mẫu.
• C. độ lệch chuẩn mẫu chia cho căn bậc hai của kích thước mẫu.

8. Sai số chuẩn của phân phối mẫu của trung bình mẫu cho một kích thước mẫu là $n$ được rút ra từ một quần thể có trung bình là $\mu$ và độ lệch chuẩn là $\sigma$ là:

• A. độ lệch chuẩn mẫu chia cho kích thước mẫu.
• B. độ lệch chuẩn mẫu chia cho căn bậc hai của kích thước mẫu.
• C. độ lệch chuẩn quần thể chia cho căn bậc hai của kích thước mẫu.

9. Giả sử rằng một quần thể có trung bình là 14 với độ lệch chuẩn là 2. Nếu một mẫu ngẫu nhiên gồm 49 quan sát được rút ra từ quần thể này, sai số chuẩn của trung bình mẫu gần đúng là:

• A. 0.04.
• B. 0.29.
• C. 2.00.

10. Trung bình của quần thể là 30 và trung bình của một mẫu có kích thước 100 là 28.5. Phương sai của mẫu là 25. Sai số chuẩn của trung bình mẫu gần đúng là:

• A. 0.05.
• B. 0.25.
• C. 0.50.

11. Điều nào sau đây ít có khả năng là một đặc tính mong muốn của một ước tính?

• A. Độ tin cậy.
• B. Hiệu quả.
• C. Tính nhất quán.

2: KHOẢNG TIN CẬY VÀ PHÂN PHỐI t

H: Phân biệt giữa ước lượng điểm và ước lượng khoảng tin cậy của một tham số tổng thể.

Ước lượng điểm là các giá trị đơn lẻ (mẫu) được sử dụng để ước lượng các tham số tổng thể. Công thức được sử dụng để tính toán ước lượng điểm được gọi là bộ ước lượng. Ví dụ, trung bình mẫu, $\bar{x}$, là một bộ ước lượng của trung bình tổng thể $\mu$ và được tính bằng công thức quen thuộc:

$$\bar{x} = \frac{\sum x}{n}$$

Giá trị được tạo ra với phép tính này cho một mẫu nhất định được gọi là ước lượng điểm của trung bình.

Một khoảng tin cậy là một khoảng giá trị mà trong đó tham số tổng thể được kỳ vọng nằm. Việc xây dựng các khoảng tin cậy sẽ được mô tả sau trong phần ôn tập chủ đề này.

I: Mô tả các thuộc tính của phân phối t của Student và tính toán và giải thích các bậc tự do của nó.

Phân phối t của Student, hay đơn giản là phân phối t, là một phân phối xác suất có hình chuông và đối xứng quanh giá trị trung bình của nó. Đây là phân phối thích hợp để sử dụng khi xây dựng các khoảng tin cậy dựa trên mẫu nhỏ (n < 30) từ các tổng thể có phương sai chưa biết và phân phối chuẩn, hoặc gần chuẩn. Nó cũng có thể thích hợp sử dụng phân phối t khi phương sai tổng thể chưa biết và kích thước mẫu đủ lớn để định lý giới hạn trung tâm đảm bảo rằng phân phối mẫu gần như phân phối chuẩn.

Phân phối t của Student có các thuộc tính sau:

• Nó đối xứng.
• Nó được xác định bởi một tham số duy nhất, bậc tự do ($df$), nơi các bậc tự do bằng số quan sát mẫu trừ 1, $n – 1$, cho các trung bình mẫu.
• Nó có nhiều xác suất ở đuôi (“đuôi dày hơn”) hơn phân phối chuẩn.
• Khi số bậc tự do (kích thước mẫu) tăng lên, hình dạng của phân phối $t$ ngày càng gần với phân phối chuẩn.

Khi so sánh với phân phối chuẩn, phân phối t phẳng hơn với nhiều diện tích dưới đuôi hơn (tức là nó có đuôi dày hơn). Tuy nhiên, khi số bậc tự do của phân phối t tăng, hình dạng của nó gần hơn với phân phối chuẩn.

Số bậc tự do cho các kiểm định dựa trên trung bình mẫu là $n – 1$ vì, khi biết trung bình, chỉ có $n – 1$ quan sát có thể là duy nhất.

Phân phối t là một phân phối đối xứng quanh điểm không. Hình dạng của phân phối t phụ thuộc vào số bậc tự do, và số bậc tự do dựa trên số lượng quan sát mẫu. Phân phối t dẹt hơn và có đuôi dày hơn so với phân phối chuẩn tắc. Khi số lượng quan sát tăng lên (tức là số bậc tự do tăng lên), phân phối $t$ trở nên nhọn hơn và đuôi của nó mỏng hơn. Khi số bậc tự do tăng lên vô hạn, phân phối t hội tụ đến phân phối chuẩn tắc ($z$-phân phối). Độ dày của đuôi so với đuôi của $z$-phân phối quan trọng trong việc kiểm định giả thuyết vì đuôi dày hơn nghĩa là có nhiều quan sát ở xa trung tâm phân phối (nhiều giá trị ngoại lai hơn). Do đó, việc kiểm định giả thuyết sử dụng phân phối $t$ làm cho khó bác bỏ giả thuyết không hơn so với việc kiểm định giả thuyết sử dụng phân phối $z$.

Bảng sau đây chứa các giá trị tới hạn một phía cho phân phối $t$ ở mức ý nghĩa 0.05 và 0.025 với các bậc tự do khác nhau ($df$). Lưu ý rằng, không giống như bảng $z$, các giá trị $t$ nằm trong bảng, và các xác suất nằm ở các tiêu đề cột. Cũng lưu ý rằng mức ý nghĩa của kiểm định $t$ tương ứng với các xác suất một phía, p, ở đầu các cột trong bảng t.

Bảng các giá trị tới hạn t

Xác suất một phía, p
df	p = 0.05	p = 0.025
5	2.015	2.571
10	1.812	2.228
15	1.753	2.131
20	1.725	2.086
25	1.708	2.060
30	1.697	2.042
40	1.684	2.021
50	1.676	2.009
60	1.671	2.000
70	1.667	1.994
80	1.664	1.990
90	1.662	1.987
100	1.660	1.984
120	1.658	1.980
∞	1.645	1.960

Hình sau minh họa các hình dạng khác nhau của phân phối $t$ liên quan đến các bậc tự do khác nhau. Xu hướng là phân phối $t$ càng giống phân phối chuẩn khi số bậc tự do tăng lên. Thực tế, số bậc tự do càng lớn, phần trăm quan sát gần trung tâm phân phối càng lớn và phần trăm quan sát ở đuôi càng nhỏ, đuôi càng mỏng khi số bậc tự do tăng lên. Điều này có nghĩa là các khoảng tin cậy cho một biến ngẫu nhiên theo phân phối $t$ phải rộng hơn (hẹp hơn) khi số bậc tự do ít (nhiều) hơn đối với một mức ý nghĩa nhất định.

Hình: Các phân phối $t$ với các bậc tự do khác nhau ($\text{df}$)

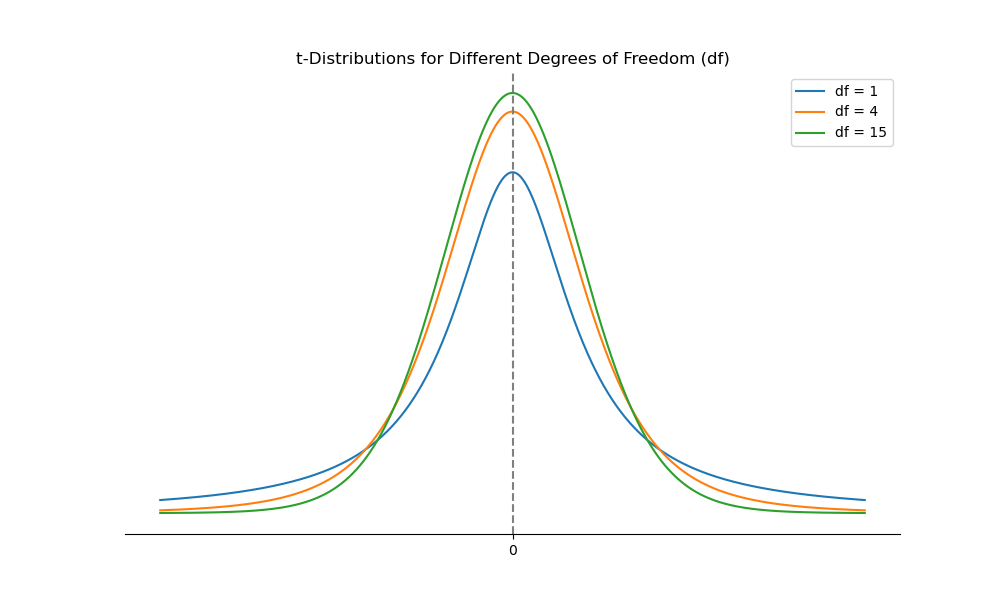
J: Tính toán và diễn giải khoảng tin cậy cho trung bình tổng thể, cho một phân phối chuẩn với 1) phương sai tổng thể đã biết, 2) phương sai tổng thể chưa biết, hoặc 3) phương sai tổng thể chưa biết và cỡ mẫu lớn.

Ước lượng khoảng tin cậy dẫn đến một phạm vi giá trị trong đó giá trị thực của một tham số sẽ nằm, với xác suất là $1 - \alpha$. Ở đây, alpha, $\alpha$, được gọi là mức ý nghĩa của khoảng tin cậy, và xác suất $1 - \alpha$ được gọi là mức độ tin cậy. Ví dụ, chúng ta có thể ước tính rằng trung bình tổng thể của các biến ngẫu nhiên sẽ nằm trong khoảng từ 15 đến 25 với mức độ tin cậy 95$\%$, hoặc ở mức ý nghĩa 5$\%$.

Khoảng tin cậy thường được xây dựng bằng cách cộng hoặc trừ một giá trị phù hợp từ ước lượng điểm. Nói chung, khoảng tin cậy có dạng:

$$\text{ước lượng điểm} \pm (\text{hệ số tin cậy} \times \text{sai số chuẩn})$$

trong đó:

• ước lượng điểm = giá trị của thống kê mẫu của tham số tổng thể
• hệ số tin cậy = số phụ thuộc vào phân phối mẫu của ước lượng điểm và xác suất rằng ước lượng điểm nằm trong khoảng tin cậy, $1 - \alpha$
• sai số chuẩn = sai số chuẩn của ước lượng điểm

Nếu tổng thể có phân phối chuẩn với phương sai đã biết, khoảng tin cậy cho trung bình tổng thể có thể được tính như sau:

$$\bar{x} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}}$$

trong đó:

• $\bar{x}$ = ước lượng điểm của trung bình tổng thể (trung bình mẫu).
• $z_{\alpha/2}$ = hệ số tin cậy, một biến ngẫu nhiên chuẩn tắc mà xác suất ở đuôi phải của phân phối là $\alpha/2$. Nói cách khác, đây là giá trị z để lại $\alpha/2$ xác suất ở đuôi trên.
• $\frac{\sigma}{\sqrt{n}}$ = sai số chuẩn của trung bình mẫu, trong đó $\sigma$ là độ lệch chuẩn đã biết của tổng thể, và $n$ là cỡ mẫu.

Các hệ số tin cậy thường được sử dụng trong phân phối chuẩn tắc chuẩn là:

$$z_{\alpha/2} = 1.645 \text{ cho khoảng tin cậy 90\% (mức ý nghĩa là 10\%, 5\% ở mỗi đuôi).}$$ $$z_{\alpha/2} = 1.960 \text{ cho khoảng tin cậy 95\% (mức ý nghĩa là 5\%, 2.5\% ở mỗi đuôi).}$$ $$z_{\alpha/2} = 2.575 \text{ cho khoảng tin cậy 99\% (mức ý nghĩa là 1\%, 0.5\% ở mỗi đuôi).}$$

Những con số này có quen thuộc không? Chúng nên như vậy! Trong phần ôn tập về các phân phối xác suất thông thường, chúng ta đã tìm thấy xác suất dưới đường cong chuẩn tắc giữa z = –1.96 và z = +1.96 là 0.95, hoặc 95%. Nhờ tính đối xứng, điều này để lại xác suất 0.025 dưới mỗi đuôi của đường cong vượt quá z = –1.96 hoặc z = +1.96, tổng cộng là 0.05, hoặc 5%—chính xác những gì chúng ta cần cho mức ý nghĩa 0.05, hoặc 5%.

VÍ DỤ: Khoảng tin cậy

Xem xét một kỳ thi thử được thực hiện bởi 36 thí sinh Cấp I. Điểm trung bình trên kỳ thi thử này là 80. Giả sử độ lệch chuẩn của tổng thể là 15, xây dựng và diễn giải khoảng tin cậy 99% cho điểm trung bình trên kỳ thi thử cho 36 thí sinh. Lưu ý rằng trong ví dụ này, độ lệch chuẩn của tổng thể đã biết, vì vậy chúng ta không cần ước lượng nó.

Trả lời: Ở mức độ tin cậy 99%, $z_{\alpha/2} = z_{0.005} = 2.58$. Vì vậy, khoảng tin cậy 99% được tính như sau:

$$\bar{x} \pm z_{\alpha/2} \frac{\sigma}{\sqrt{n}} = 80 \pm 2.58 \frac{15}{\sqrt{36}} = 80 \pm 6.45$$

Vì vậy, khoảng tin cậy 99% dao động từ 73.55 đến 86.45.

VÍ DỤ: Khoảng tin cậy cho trung bình tổng thể và cho một quan sát đơn lẻ

Lợi nhuận hàng năm của cổ phiếu năng lượng phân phối xấp xỉ theo chuẩn với trung bình là 9% và độ lệch chuẩn là 6%. Xây dựng khoảng tin cậy 90% cho lợi nhuận hàng năm của một cổ phiếu năng lượng được chọn ngẫu nhiên và khoảng tin cậy 90% cho trung bình lợi nhuận hàng năm của mẫu 12 cổ phiếu năng lượng.

Trả lời: Khoảng tin cậy 90% cho một quan sát đơn lẻ là 1.645 độ lệch chuẩn từ trung bình mẫu.

$$9\% \pm 1.645(6\%) = -0.87\% \text{ đến } 18.87\%$$

Khoảng tin cậy 90% cho trung bình tổng thể là 1.645 sai số chuẩn từ trung bình mẫu.

$$9\% \pm 1.645 \left( \frac{6\%}{\sqrt{12}} \right) = 6.15\% \text{ đến } 11.85\%$$

Khoảng tin cậy có thể được diễn giải theo quan điểm xác suất hoặc quan điểm thực tiễn. Đối với kết quả của ví dụ kỳ thi thực hành $\text{CFA}^\circledR$, hai quan điểm này có thể được mô tả như sau:

• Diễn giải xác suất. Sau khi lấy mẫu nhiều lần từ các thí sinh CFA, thực hiện kỳ thi thử, và xây dựng khoảng tin cậy cho trung bình của mỗi mẫu, 99% của các khoảng tin cậy kết quả sẽ, về lâu dài, bao gồm trung bình tổng thể.
• Diễn giải thực tiễn. Chúng ta tin tưởng 99% rằng điểm trung bình tổng thể nằm trong khoảng từ 73.55 đến 86.45 cho các thí sinh từ tổng thể này.

Khoảng Tin Cậy Cho Trung Bình Tổng Thể: Phân Phối Chuẩn Với Phương Sai Không Biết

Nếu phân phối của tổng thể là phân phối chuẩn với phương sai không biết, chúng ta có thể sử dụng phân phối t để xây dựng khoảng tin cậy:

$$\bar{x} \pm t_{\alpha/2} \frac{s}{\sqrt{n}}$$

trong đó:

• $\bar{x}$ = ước lượng điểm của trung bình tổng thể
• $t_{\alpha/2}$ = hệ số tin cậy (còn gọi là giá trị t hoặc giá trị tới hạn t) tương ứng với biến ngẫu nhiên phân phối t với bậc tự do là $n - 1$, trong đó $n$ là kích thước mẫu. Diện tích dưới đuôi của phân phối t về bên phải của $t_{\alpha/2}$ là $\alpha/2$
• $\frac{s}{\sqrt{n}}$ = sai số chuẩn của trung bình mẫu
• $s$ = độ lệch chuẩn mẫu

Không giống như phân phối chuẩn chuẩn tắc, các hệ số tin cậy cho phân phối t phụ thuộc vào kích thước mẫu, vì vậy chúng ta không thể dựa vào một bộ hệ số tin cậy thường dùng. Thay vào đó, các hệ số tin cậy cho phân phối t phải được tra cứu trong bảng phân phối t của Student, như bảng ở cuối cuốn sách này.

Do đuôi của phân phối t tương đối lớn hơn, các khoảng tin cậy được xây dựng bằng cách sử dụng các hệ số tin cậy t $(t_{\alpha/2})$ sẽ bảo thủ hơn (rộng hơn) so với các khoảng tin cậy được xây dựng bằng cách sử dụng các hệ số tin cậy z $(z_{\alpha/2})$.

VÍ DỤ: Khoảng tin cậy

Hãy trở lại với ví dụ của McCrary, Inc. Nhớ lại rằng chúng ta đã lấy mẫu 30 lần lợi tức cổ phiếu hàng tháng gần đây của McCrary, Inc. và xác định rằng lợi tức trung bình là 2% và độ lệch chuẩn mẫu là 20%. Vì phương sai tổng thể không biết, sai số chuẩn của mẫu được ước lượng là: $s_{\bar{x}} = \frac{s}{\sqrt{n}} = \frac{20\%}{\sqrt{30}} = 3.65\%$

Bây giờ, hãy xây dựng một khoảng tin cậy 95% cho lợi tức trung bình hàng tháng.

Trả lời: Ở đây, chúng ta sẽ sử dụng hệ số tin cậy vì phương sai tổng thể không biết. Vì có 30 quan sát, bậc tự do là $n - 1 = 30 - 1 = 29$. Nhớ rằng, vì đây là kiểm tra hai phía, ở mức độ tin cậy 95%, xác suất dưới mỗi đuôi phải là $\alpha/2 = 2.5\%$, tổng cộng là 5%. Vì vậy, tra cứu các xác suất một phía cho phân phối t của Student ở cuối cuốn sách này, chúng ta tìm giá trị t tới hạn (hệ số tin cậy) tại $\alpha/2 = 0.025$ và $n - 1 = 29$ là $t_{\alpha/2} = 2.045$. Do đó, khoảng tin cậy 95% cho trung bình tổng thể là: $2\% \pm (t_{\alpha/2} \cdot s_{\bar{x}}) = 2\% \pm 2.045 (3.65\%) = 2\% \pm 7.4\%$

Do đó, khoảng tin cậy 95% có giới hạn dưới là -5.4% và giới hạn trên là 9.4%.

Chúng ta có thể diễn giải khoảng tin cậy này bằng cách nói rằng chúng ta tin tưởng 95% rằng lợi tức trung bình hàng tháng của cổ phiếu McCrary nằm trong khoảng từ -5.4% đến 9.4%.

GHI CHÚ CỦA GIÁO SƯ

Bạn nên luyện tập tra cứu các hệ số tin cậy (tức là giá trị t tới hạn hoặc giá trị t) trong bảng t. Bước đầu tiên luôn là tính toán bậc tự do, là $n - 1$. Bước thứ hai là tìm mức độ alpha hoặc mức ý nghĩa phù hợp. Điều này phụ thuộc vào việc kiểm tra bạn đang quan tâm là một phía (như ví dụ của chúng ta) hay hai phía (như ví dụ của chúng ta).

Khoảng tin cậy cho Trung bình Quần thể Khi Phương sai Quần thể Không biết Được Mẫu Lớn Từ Bất kỳ Loại Phân phối Nào

Chúng ta hiện đã biết rằng thống kê $z$ nên được sử dụng để xây dựng khoảng tin cậy khi phân phối quần thể là chuẩn và phương sai được biết, và thống kê $t$ nên được sử dụng khi phân phối là chuẩn nhưng phương sai không biết. Nhưng chúng ta làm gì khi phân phối không chuẩn?

Hóa ra, kích thước mẫu ảnh hưởng đến việc liệu chúng ta có thể xây dựng khoảng tin cậy thích hợp cho trung bình mẫu hay không.

• Nếu phân phối là chuẩn nhưng phương sai quần thể không biết, thống kê $z$ có thể được sử dụng miễn là kích thước mẫu lớn ($n \ge 30$). Chúng ta có thể làm điều này vì định lý giới hạn trung tâm đảm bảo rằng phân phối của trung bình mẫu xấp xỉ chuẩn khi mẫu lớn.
• Nếu phân phối không chuẩn và phương sai quần thể không biết, thống kê $t$ có thể được sử dụng miễn là kích thước mẫu lớn ($n \ge 30$). Cũng có thể chấp nhận sử dụng thống kê $z$, mặc dù sử dụng thống kê $t$ thận trọng hơn.

Điều này có nghĩa là nếu chúng ta lấy mẫu từ một phân phối không chuẩn (đôi khi là trường hợp trong tài chính), chúng ta không thể tạo khoảng tin cậy nếu kích thước mẫu nhỏ hơn 30. Vì vậy, tất cả các yếu tố khác đều như nhau, hãy đảm bảo bạn có một mẫu ít nhất là 30, và càng lớn càng tốt.

LƯU Ý CỦA GIÁO SƯ

Bạn nên ghi nhớ các tiêu chí trong bảng sau.

Bảng: Tiêu chí Chọn Thống kê Thử nghiệm Thích hợp

	Thống kê Thử nghiệm	Thống kê Thử nghiệm
Khi lấy mẫu từ:	Mẫu Nhỏ ($n < 30$)	Mẫu Lớn ($n \ge 30$)
Phân phối chuẩn với phương sai biết	thống kê z	thống kê z
Phân phối chuẩn với phương sai không biết	thống kê t	thống kê t
Phân phối không chuẩn với phương sai biết	không khả dụng	thống kê z
Phân phối không chuẩn với phương sai không biết	không khả dụng	thống kê t

Lưu ý: Thống kê $t$ về mặt lý thuyết có thể chấp nhận ở đây, nhưng sử dụng thống kê $t$ thận trọng hơn.

Tất cả các phân tích trước đây phụ thuộc vào việc mẫu chúng ta lấy từ quần thể là ngẫu nhiên. Nếu mẫu không ngẫu nhiên, định lý giới hạn trung tâm không áp dụng, ước tính của chúng ta sẽ không có các tính chất mong muốn, và chúng ta không thể tạo các khoảng tin cậy không thiên lệch. Điều ngạc nhiên là, tạo một mẫu ngẫu nhiên không dễ dàng như người ta tin. Có nhiều sai lầm tiềm tàng trong các phương pháp lấy mẫu có thể gây thiên lệch kết quả. Những thiên lệch này đặc biệt gây rắc rối trong nghiên cứu tài chính, nơi dữ liệu lịch sử sẵn có rất nhiều, nhưng việc tạo dữ liệu mẫu mới thông qua thí nghiệm bị hạn chế.

K: Mô tả các vấn đề liên quan đến việc lựa chọn kích thước mẫu phù hợp, sai lệch do khai thác dữ liệu, sai lệch do lựa chọn mẫu, sai lệch do tồn tại, sai lệch do nhìn trước, và sai lệch do khoảng thời gian.

Chúng ta đã thấy rằng một mẫu lớn hơn sẽ giảm sai số mẫu và độ lệch chuẩn của thống kê mẫu xung quanh giá trị thật (giá trị tổng thể) của nó. Khoảng tin cậy sẽ hẹp hơn khi mẫu lớn hơn và sai số chuẩn của các ước lượng điểm của các tham số tổng thể sẽ ít hơn.

Có hai giới hạn đối với ý tưởng "càng lớn càng tốt" khi chọn kích thước mẫu phù hợp. Một là các mẫu lớn hơn có thể chứa các quan sát từ một tổng thể khác (phân phối khác). Nếu chúng ta bao gồm các quan sát từ một tổng thể khác (một tổng thể có tham số tổng thể khác), chúng ta sẽ không nhất thiết cải thiện, và có thể thậm chí giảm, độ chính xác của các ước lượng tham số tổng thể của mình. Cân nhắc thứ hai là chi phí. Chi phí sử dụng một mẫu lớn hơn phải được cân nhắc với giá trị của việc tăng độ chính xác từ việc tăng kích thước mẫu. Cả hai yếu tố này đều gợi ý rằng kích thước mẫu lớn nhất có thể không phải luôn là lựa chọn phù hợp nhất.

Thiên Kiến Khai Phá Dữ Liệu, Thiên Kiến Chọn Mẫu, Thiên Kiến Tồn Tại, Thiên Kiến Nhìn Trước và Thiên Kiến Thời Gian

Khai phá dữ liệu xảy ra khi các nhà phân tích liên tục sử dụng cùng một cơ sở dữ liệu để tìm kiếm các mẫu hoặc quy tắc giao dịch cho đến khi phát hiện ra một mẫu "hoạt động". Ví dụ, nghiên cứu thực nghiệm đã cung cấp bằng chứng rằng các cổ phiếu giá trị có vẻ vượt trội hơn các cổ phiếu tăng trưởng. Một số nhà nghiên cứu cho rằng hiện tượng này thực chất là sản phẩm của việc khai phá dữ liệu. Vì tập dữ liệu của lợi nhuận cổ phiếu lịch sử khá hạn chế, nên khó có thể biết chắc chắn liệu sự khác biệt giữa lợi nhuận cổ phiếu giá trị và tăng trưởng có phải là hiện tượng kinh tế thực sự hay chỉ là một mẫu ngẫu nhiên được phát hiện sau khi liên tục tìm kiếm bất kỳ mẫu nào có thể nhận biết trong dữ liệu.

Thiên kiến khai phá dữ liệu đề cập đến các kết quả mà độ tin cậy thống kê của mẫu được đánh giá quá cao vì các kết quả được tìm thấy thông qua khai phá dữ liệu.

Khi đọc các phát hiện nghiên cứu gợi ý một chiến lược giao dịch có lợi nhuận, hãy đảm bảo chú ý đến các dấu hiệu cảnh báo sau về việc khai phá dữ liệu:

• Bằng chứng cho thấy nhiều biến số khác nhau đã được thử nghiệm, hầu hết trong số đó không được báo cáo, cho đến khi tìm thấy các biến số có ý nghĩa.
• Thiếu bất kỳ lý thuyết kinh tế nào phù hợp với các kết quả thực nghiệm.

Cách tốt nhất để tránh khai phá dữ liệu là kiểm tra một quy tắc giao dịch có thể có lợi nhuận trên một tập dữ liệu khác với tập dữ liệu mà bạn đã sử dụng để phát triển quy tắc đó (tức là, sử dụng dữ liệu ngoài mẫu).

Thiên kiến chọn mẫu xảy ra khi một số dữ liệu bị loại bỏ một cách có hệ thống khỏi phân tích, thường là do không có sẵn. Thực tiễn này làm cho mẫu quan sát được trở nên không ngẫu nhiên, và bất kỳ kết luận nào rút ra từ mẫu này không thể áp dụng cho dân số vì mẫu quan sát được và phần dân số không được quan sát là khác nhau.

Thiên kiến tồn tại là dạng phổ biến nhất của thiên kiến chọn mẫu. Một ví dụ điển hình về sự tồn tại của thiên kiến tồn tại trong đầu tư là nghiên cứu về hiệu suất quỹ tương hỗ. Hầu hết các cơ sở dữ liệu quỹ tương hỗ, như Morningstar®, chỉ bao gồm các quỹ hiện đang tồn tại - các "người sống sót". Họ không bao gồm các quỹ đã ngừng tồn tại do đóng cửa hoặc hợp nhất.

Điều này sẽ không thành vấn đề nếu các đặc điểm của các quỹ sống sót và các quỹ bị thiếu là giống nhau; khi đó mẫu của các quỹ sống sót vẫn sẽ là một mẫu ngẫu nhiên được rút ra từ tổng thể các quỹ tương hỗ. Tuy nhiên, như người ta mong đợi, và như bằng chứng đã chỉ ra, các quỹ bị loại khỏi mẫu có lợi nhuận thấp hơn so với các quỹ sống sót. Do đó, mẫu sống sót bị thiên vị về phía các quỹ tốt hơn (tức là không ngẫu nhiên). Phân tích một mẫu quỹ tương hỗ có thiên kiến tồn tại sẽ cho ra kết quả ước tính quá cao về lợi nhuận trung bình của quỹ tương hỗ vì cơ sở dữ liệu chỉ bao gồm các quỹ hoạt động tốt hơn. Giải pháp cho thiên kiến tồn tại là sử dụng một mẫu của các quỹ bắt đầu vào cùng một thời điểm và không loại bỏ các quỹ đã bị loại khỏi mẫu.

Thiên kiến nhìn trước xảy ra khi một nghiên cứu kiểm tra một mối quan hệ sử dụng dữ liệu mẫu không có sẵn vào ngày kiểm tra. Ví dụ, hãy xem xét việc kiểm tra một quy tắc giao dịch dựa trên tỷ lệ giá trị sổ sách vào cuối năm tài chính. Giá cổ phiếu có sẵn cho tất cả các công ty tại cùng một thời điểm, trong khi giá trị sổ sách cuối năm có thể không có sẵn cho đến 30 đến 60 ngày sau khi năm tài chính kết thúc. Để giải quyết thiên kiến này, một nghiên cứu sử dụng tỷ lệ giá trị sổ sách để kiểm tra các chiến lược giao dịch có thể ước tính giá trị sổ sách được báo cáo vào cuối năm tài chính và giá trị thị trường hai tháng sau đó.

Thiên kiến thời gian có thể xảy ra nếu khoảng thời gian mà dữ liệu được thu thập quá ngắn hoặc quá dài. Nếu khoảng thời gian quá ngắn, kết quả nghiên cứu có thể phản ánh các hiện tượng cụ thể của khoảng thời gian đó, hoặc có thể là khai phá dữ liệu. Nếu khoảng thời gian quá dài, các mối quan hệ kinh tế cơ bản làm nền tảng cho kết quả có thể đã thay đổi.

Ví dụ, các kết quả nghiên cứu có thể chỉ ra rằng các cổ phiếu nhỏ vượt trội hơn các cổ phiếu lớn trong giai đoạn 1980-1985. Điều này có thể là kết quả của thiên kiến thời gian - trong trường hợp này, sử dụng khoảng thời gian quá ngắn. Không rõ liệu mối quan hệ này sẽ tiếp tục trong tương lai hay chỉ là một sự kiện riêng lẻ.

Mặt khác, một nghiên cứu định lượng mối quan hệ giữa lạm phát và thất nghiệp trong giai đoạn từ 1940-2000 cũng sẽ dẫn đến thiên kiến thời gian - vì giai đoạn này quá dài, và nó bao gồm một sự thay đổi cơ bản trong mối quan hệ giữa lạm phát và thất nghiệp xảy ra vào những năm 1980. Trong trường hợp này, dữ liệu nên được chia thành hai mẫu con bao gồm giai đoạn trước và sau khi thay đổi.

📝 LUYỆN TẬP

1. Điều nào sau đây ít có khả năng là một đặc tính của phân phối Student’s t?

• A. Khi bậc tự do càng lớn, phương sai càng tiến đến 0.
• B. Nó được xác định bởi một tham số duy nhất, bậc tự do, bằng $n - 1$.
• C. Nó có nhiều xác suất ở đuôi và ít ở đỉnh hơn so với phân phối chuẩn.

2. Một mẫu ngẫu nhiên gồm 100 khách hàng của cửa hàng máy tính đã chi tiêu trung bình $75 tại cửa hàng. Giả sử phân phối là bình thường và độ lệch chuẩn của dân số là $20, khoảng tin cậy 95% cho trung bình dân số gần nhất với:

• A. $71.08 đến $78.92.
• B. $73.08 đến $80.11.
• C. $54.55 đến $79.44.

3. Best Computers, Inc., bán máy tính và các bộ phận máy tính qua thư. Một mẫu gồm 25 đơn hàng gần đây cho thấy thời gian trung bình để gửi các đơn hàng này là 70 giờ với độ lệch chuẩn mẫu là 14 giờ. Giả sử dân số được phân phối bình thường, khoảng tin cậy 99% cho trung bình dân số là:

• A. 70 ± 2.80 giờ.
• B. 70 ± 6.98 giờ.
• C. 70 ± 7.83 giờ.

4. Thống kê kiểm định nào thích hợp nhất để xây dựng khoảng tin cậy cho trung bình dân số khi dân số được phân phối bình thường, nhưng phương sai chưa biết?

• A. Thống kê $z$ tại $\alpha$ với $n$ độ tự do.
• B. Thống kê $t$ tại $\alpha/2$ với $n1$ độ tự do.
• C. Thống kê $t$ tại $\alpha/2$ với $n - 1$ độ tự do.

5. Khi xây dựng khoảng tin cậy cho trung bình dân số của một phân phối không bình thường khi phương sai dân số chưa biết và kích thước mẫu lớn ($n > 30$), một nhà phân tích có thể chấp nhận sử dụng:

• A. Hoặc thống kê $z$ hoặc thống kê $t$.
• B. Chỉ thống kê $z$ tại $\alpha$ với $n$ độ tự do.
• C. Chỉ thống kê $t$ tại $\alpha / 2$ với $n$ độ tự do.

6. Jenny Fox đánh giá các nhà quản lý có độ lệch chuẩn dân số của tỷ suất lợi nhuận là 8%. Nếu các tỷ suất lợi nhuận độc lập giữa các nhà quản lý, Jenny cần mẫu lớn bao nhiêu để sai số chuẩn của trung bình mẫu là 1.26%?

• A. 7.
• B. 30.
• C. 40.

7. Tỷ suất lợi nhuận hàng năm trên cổ phiếu nhỏ có trung bình dân số là 12% và độ lệch chuẩn dân số là 20%. Nếu các tỷ suất lợi nhuận được phân phối bình thường, khoảng tin cậy 90% cho tỷ suất lợi nhuận trung bình trong 5 năm là:

• A. 5.40% đến 18.60%.
• B. –2.75% đến 26.76%.
• C. –5.52% đến 29.52%.

8. Một nhà phân tích sử dụng dữ liệu lịch sử không được công khai vào thời kỳ được nghiên cứu sẽ có một mẫu với:

• A. Thiên lệch xem trước.
• B. Thiên lệch thời kỳ.
• C. Thiên lệch chọn mẫu.

9. Thiên lệch nào có liên quan chặt chẽ nhất với thiên lệch sống sót?

• A. Các nghiên cứu giá trị sổ sách.
• B. Các nghiên cứu chọn mẫu trái phiếu.
• C. Các nghiên cứu về hiệu suất của quỹ tương hỗ.