Giá trị thời gian của tiền

A. Diễn giải lãi suất như là tỷ lệ lợi nhuận yêu cầu, tỷ lệ chiết khấu, hoặc chi phí cơ hội.

Lãi suất là thước đo giá trị thời gian của tiền, mặc dù sự khác biệt về rủi ro trong các chứng khoán tài chính dẫn đến sự khác biệt trong lãi suất cân bằng của chúng. Lãi suất cân bằng là tỷ lệ lợi nhuận yêu cầu cho một khoản đầu tư cụ thể, theo nghĩa là tỷ lệ lợi nhuận thị trường là lợi nhuận mà các nhà đầu tư và người tiết kiệm yêu cầu để họ sẵn lòng cho vay tiền của mình.

Lãi suất cũng được gọi là tỷ lệ chiết khấu và trên thực tế, các thuật ngữ này thường được sử dụng thay thế cho nhau. Nếu một cá nhân có thể vay tiền với lãi suất 10%, thì cá nhân đó nên chiết khấu các khoản thanh toán sẽ được thực hiện trong tương lai ở mức lãi suất đó để có được giá trị tương đương của chúng bằng đô la hiện tại hoặc các loại tiền tệ khác.

Cuối cùng, chúng ta cũng có thể xem lãi suất như là chi phí cơ hội của việc tiêu dùng hiện tại. Nếu tỷ lệ lãi suất thị trường trên các chứng khoán một năm là 5%, thì việc kiếm thêm 5% là chi phí cơ hội bị bỏ qua khi tiêu dùng hiện tại được chọn thay vì tiết kiệm (hoãn tiêu dùng).

B. Giải thích lãi suất như là tổng của tỷ lệ lãi suất thực phi rủi ro, lạm phát kỳ vọng và các phần bù bồi thường cho nhà đầu tư về các loại rủi ro riêng biệt.

Tỷ lệ lãi suất thực phi rủi ro là một tỷ lệ lý thuyết trên một khoản vay một kỳ mà không có kỳ vọng lạm phát trong đó. Khi chúng ta nói về tỷ lệ lợi nhuận thực, chúng ta đề cập đến sự gia tăng sức mua của nhà đầu tư (sau khi điều chỉnh lạm phát). Vì lạm phát kỳ vọng trong các kỳ tương lai không phải là không, nên các tỷ lệ mà chúng ta quan sát được trên các trái phiếu kho bạc Hoa Kỳ (T-bills), ví dụ như, là các tỷ lệ phi rủi ro nhưng không phải là tỷ lệ lợi nhuận thực. Các tỷ lệ T-bill là tỷ lệ phi rủi ro danh nghĩa vì chúng chứa một phần bù lạm phát. Mối quan hệ gần đúng ở đây là:

$$\text{tỷ lệ phi rủi ro danh nghĩa} = \text{tỷ lệ lãi suất thực phi rủi ro} + \text{tỷ lệ lạm phát kỳ vọng}$$

Chứng khoán có thể có một hoặc nhiều loại rủi ro, và mỗi rủi ro bổ sung sẽ tăng tỷ lệ lợi nhuận yêu cầu trên chứng khoán. Các loại rủi ro này là:

• Rủi ro vỡ nợ (default risk) . Rủi ro rằng người vay sẽ không thực hiện các khoản thanh toán đã hứa đúng hạn.
• Rủi ro thanh khoản (liquidity risk). Rủi ro nhận được ít hơn giá trị hợp lý cho một khoản đầu tư nếu nó phải được bán nhanh chóng để lấy tiền mặt.
• Rủi ro đáo hạn (maturity risk). Như chúng ta sẽ đề cập chi tiết trong phần về chứng khoán nợ, giá của các trái phiếu dài hạn biến động nhiều hơn so với các trái phiếu ngắn hạn. Trái phiếu có thời gian đáo hạn dài hơn có rủi ro đáo hạn nhiều hơn so với trái phiếu ngắn hạn và yêu cầu một phần bù rủi ro đáo hạn.

Mỗi yếu tố rủi ro này đều được gắn liền với một phần bù rủi ro (risk premium) mà chúng ta thêm vào tỷ lệ phi rủi ro danh nghĩa để điều chỉnh cho rủi ro vỡ nợ lớn hơn, thanh khoản kém hơn và thời gian đáo hạn dài hơn so với một tỷ lệ phi rủi ro ngắn hạn, rất thanh khoản như tỷ lệ trên T-bills. Chúng ta có thể viết:

$$\begin{align*} \text{tỷ lệ lãi suất yêu cầu trên chứng khoán} &= \text{tỷ lệ phi rủi ro danh nghĩa} \\ &+ \text{phần bù rủi ro vỡ nợ} \\ &+ \text{phần bù thanh khoản} \\ &+ \text{phần bù rủi ro đáo hạn} \end{align*}$$

C. Tính toán và diễn giải lãi suất hiệu quả hàng năm (EAR), dựa trên lãi suất hàng năm được công bố và tần suất ghép lãi, và giải quyết các vấn đề về giá trị thời gian của tiền khi các kỳ ghép lãi không phải hàng năm.

Các tổ chức tài chính thường công bố lãi suất dưới dạng lãi suất hàng năm, cùng với tần suất ghép lãi, thay vì công bố lãi suất dưới dạng lãi suất định kỳ — lãi suất kiếm được trong một kỳ ghép lãi.

Ví dụ, một ngân hàng sẽ công bố lãi suất tiết kiệm là 8%, ghép lãi hàng quý, thay vì 2% mỗi quý. Lãi suất mà nhà đầu tư thực sự nhận được do ghép lãi được gọi là lãi suất hiệu quả hàng năm (EAR). EAR đại diện cho tỷ suất lợi nhuận hàng năm thực tế nhận được sau khi đã điều chỉnh cho các kỳ ghép lãi khác nhau.

EAR có thể được xác định như sau:

$$\text{EAR} = (1 + \text{lãi suất định kỳ})^m - 1$$

trong đó:

• $\text{lãi suất định kỳ} = \frac{\text{lãi suất hàng năm được công bố}}{m}$
• $m = \text{số kỳ ghép lãi trong một năm}$

Rõ ràng, EAR cho một lãi suất công bố là 8% ghép lãi hàng năm không giống như EAR cho 8% ghép lãi nửa năm, hoặc hàng quý. Thật vậy, bất cứ khi nào lãi suất kép được sử dụng, lãi suất công bố và lãi suất thực tế (hiệu quả) chỉ bằng nhau khi lãi suất được ghép hàng năm. Nếu không, tần suất ghép lãi càng lớn thì EAR càng cao so với lãi suất công bố.

Việc tính toán EAR là cần thiết khi so sánh các khoản đầu tư có các kỳ ghép lãi khác nhau. Nó cho phép so sánh tỷ lệ lãi suất một cách đồng đều.

Ví dụ: Tính toán EAR

Tính EAR nếu lãi suất hàng năm được công bố là $12\%$, ghép lãi hàng quý.

Trả lời: Ở đây m = 4, do đó lãi suất định kỳ là $\frac{12}{4} = 3\%$.

Do đó, $\text{EAR} = (1 + 0.03)^4 - 1 = 1.1255 - 1 = 0.1255 = 12.55\%$.

Giải pháp này sử dụng phím [y^x] trên máy tính tài chính của bạn.

Các bước chính xác trên TI để tính toán trên là 1.03 [y^x] 4 [=].

Trên HP, các bước là 1.03 [ENTER] 4 [y^x].

Ví dụ: Tính toán EAR cho một loạt các tần suất ghép lãi

Sử dụng lãi suất công bố là 6%, tính toán EAR cho các tần suất ghép lãi nửa năm, hàng quý, hàng tháng và hàng ngày.

Trả lời:

EAR với:

• ghép lãi nửa năm = (1 + 0.03)^2 - 1 = 1.06090 - 1 = 0.06090 = 6.090%
• ghép lãi hàng quý = (1 + 0.015)^4 - 1 = 1.06136 - 1 = 0.06136 = 6.136%
• ghép lãi hàng tháng = (1 + 0.005)^12 - 1 = 1.06168 - 1 = 0.06168 = 6.168%
• ghép lãi hàng ngày = (1 + 0.00016438)^365 - 1 = 1.06183 - 1 = 0.06183 = 6.183%

Lưu ý rằng EAR tăng lên khi tần suất ghép lãi tăng lên.

Giới hạn của các kỳ ghép lãi ngắn hơn và ngắn hơn được gọi là ghép lãi liên tục. Để chuyển đổi lãi suất hàng năm sang EAR với ghép lãi liên tục, chúng ta sử dụng công thức $e^r - 1 = \text{EAR}$.

Với 6%, chúng ta có $e^{0.06} - 1 = 6.1837\%$. Các bước tính toán là 0.06 [2nd] [e^x] [−] 1 [=] = 0.061837.

D. Tính toán và giải thích giá trị tương lai (FV) và giá trị hiện tại (PV) của một khoản tiền đơn lẻ, niên kim thông thường, niên kim đến hạn, vĩnh viễn (chỉ PV), và một chuỗi các dòng tiền không đều nhau.

Giá trị tương lai của một khoản tiền đơn lẻ

Giá trị tương lai là số tiền mà một khoản tiền gửi hiện tại sẽ tăng lên theo thời gian khi nó được đặt trong một tài khoản trả lãi kép. FV, còn được gọi là giá trị kép, đơn giản là một ví dụ về lãi kép hoạt động.

Công thức cho FV của một dòng tiền đơn lẻ là:

$$FV = PV(1 + I/Y)^N$$

trong đó:

• $PV$ = số tiền đầu tư hôm nay (giá trị hiện tại)
• $I/Y$ = tỷ suất lợi nhuận mỗi kỳ ghép lãi
• $N$ = tổng số kỳ ghép lãi

Trong biểu thức này, đầu tư liên quan đến một dòng tiền ra đơn lẻ, PV, xảy ra hôm nay, tại t = 0 trên dòng thời gian. Công thức FV cho một khoản tiền đơn lẻ sẽ xác định giá trị của khoản đầu tư vào cuối các kỳ ghép lãi N, với giả định rằng nó có thể kiếm được một tỷ suất lợi nhuận ghép lãi hoàn toàn, I/Y, trong suốt các kỳ hạn.

Hệ số $(1 + I/Y)^N$ đại diện cho tỷ lệ ghép lãi trên một khoản đầu tư và thường được gọi là hệ số giá trị tương lai, hoặc hệ số lãi suất giá trị tương lai, cho một dòng tiền đơn lẻ tại I/Y trong các kỳ ghép lãi N. Đây là các giá trị xuất hiện trong các bảng hệ số lãi suất, mà chúng ta sẽ không sử dụng.

Ví dụ: FV của một khoản tiền đơn lẻ

Tính toán FV của một khoản đầu tư $300 vào cuối mười năm nếu nó kiếm được tỷ suất lợi nhuận ghép lãi hàng năm là 8%.

Trả lời:

Để giải quyết vấn đề này với máy tính của bạn, nhập dữ liệu liên quan và tính toán FV.

$N = 10; I/Y = 8; PV = -300; CPT → FV = 647.68$

Ghi chú của Giáo sư: Lưu ý dấu âm trên PV. Điều này không cần thiết, nhưng nó làm cho FV ra một số dương. Nếu bạn nhập PV là một số dương, hãy bỏ qua dấu âm xuất hiện trên FV.

Vấn đề tương đối đơn giản này cũng có thể được giải quyết bằng cách sử dụng phương trình sau.

$FV = 300(1 + 0.08)^{10} = 647.68$

Trên máy tính TI, nhập 1.08 [yx] 10 [x] 300 [=].

Giá trị hiện tại của một khoản tiền đơn lẻ

PV của một khoản tiền đơn lẻ là giá trị hôm nay của một dòng tiền sẽ được nhận vào một thời điểm nào đó trong tương lai. Nói cách khác, đó là số tiền phải đầu tư hôm nay, với một tỷ suất lợi nhuận nhất định trong một khoảng thời gian nhất định, để có được một FV xác định. Như đã đề cập trước đó, quá trình tìm PV của một dòng tiền được gọi là chiết khấu (tức là các dòng tiền tương lai được “chiết khấu” trở lại hiện tại). Tỷ suất lợi nhuận sử dụng trong quá trình chiết khấu thường được gọi là tỷ lệ chiết khấu nhưng cũng có thể được gọi là chi phí cơ hội, tỷ suất lợi nhuận yêu cầu, và chi phí vốn. Dù bạn muốn gọi nó là gì, nó đại diện cho tỷ suất lợi nhuận kép hàng năm có thể kiếm được từ một khoản đầu tư.

Mối quan hệ giữa PV và FV có thể được thấy bằng cách xem xét biểu thức FV đã nêu trước đó. Viết lại phương trình FV dưới dạng PV, chúng ta có:

$$PV = FV \times \left[ \frac{1}{(1 + I/Y)^N} \right] = \frac{FV}{(1 + I/Y)^N}$$

Lưu ý rằng đối với một dòng tiền tương lai đơn lẻ, PV luôn nhỏ hơn FV bất cứ khi nào tỷ lệ chiết khấu là dương.

Lượng $1/(1 + I/Y)^N$ trong phương trình PV thường được gọi là hệ số giá trị hiện tại, hệ số lãi suất giá trị hiện tại, hoặc hệ số chiết khấu cho một dòng tiền đơn lẻ tại $I/Y$ trong các kỳ ghép lãi $N$.

Ví dụ: PV của một khoản tiền đơn lẻ

Với tỷ lệ chiết khấu là 9%, tính toán PV của một dòng tiền $1,000 sẽ được nhận trong năm năm.

Trả lời:

Để giải quyết vấn đề này, nhập dữ liệu liên quan và tính toán PV.

$N = 5; I/Y = 9; FV = 1,000; CPT → PV = -649.93 \text{(bỏ qua dấu)}$

Ghi chú của Giáo sư: Với các vấn đề PV đơn lẻ, bạn có thể nhập FV là một số dương và bỏ qua dấu âm trên PV hoặc nhập FV là một số âm.

Vấn đề tương đối đơn giản này cũng có thể được giải quyết bằng cách sử dụng phương trình PV sau.

$PV = 1,000 / (1 + 0.09)^5 = 649.93$

Trên TI, nhập 1.09 [yx] 5 [=] [1/x] [x] 1,000 [=].

PV được tính toán ở đây ngụ ý rằng với tỷ lệ 9%, một nhà đầu tư sẽ không phân biệt giữa $1,000 trong năm năm và $649.93 hôm nay. Nói cách khác, $649.93 là số tiền phải đầu tư hôm nay với tỷ suất lợi nhuận 9% để tạo ra dòng tiền $1,000 vào cuối năm năm.

Niên kim

Một niên kim là một dòng dòng tiền bằng nhau xuất hiện tại khoảng thời gian bằng nhau trong một khoảng thời gian nhất định. Nhận $1,000 mỗi năm vào cuối mỗi năm trong tám năm tới là một ví dụ về niên kim. Có hai loại niên kim: niên kim thông thường và niên kim đến hạn. Niên kim thông thường là loại niên kim phổ biến nhất. Nó được đặc trưng bởi các dòng tiền xuất hiện vào cuối mỗi kỳ hạn. Đây là một mẫu dòng tiền điển hình cho nhiều ứng dụng đầu tư và tài chính doanh nghiệp. Loại niên kim khác được gọi là niên kim đến hạn, trong đó các khoản thanh toán hoặc nhận tiền xuất hiện vào đầu mỗi kỳ hạn (tức là, khoản thanh toán đầu tiên là hôm nay tại t = 0).

Tính toán giá trị hiện tại (PV) hoặc giá trị tương lai (FV) của một niên kim bằng máy tính của bạn không khó hơn so với một dòng tiền đơn lẻ. Bạn sẽ biết bốn trong năm biến số liên quan và giải cho biến thứ năm (hoặc PV hoặc FV). Sự khác biệt giữa các bài toán giá trị hiện tại (TVM) của số tiền đơn lẻ và niên kim là thay vì giải PV hoặc FV của một dòng tiền đơn lẻ, chúng ta giải PV hoặc FV của một dòng tiền định kỳ bằng nhau, trong đó kích thước của dòng tiền định kỳ được xác định bởi biến thanh toán (PMT) trên máy tính của bạn.

Ví dụ: Giá trị tương lai của niên kim thông thường

Giá trị tương lai của một niên kim thông thường trả $150 mỗi năm vào cuối mỗi năm trong 15 năm tới, với mức lợi nhuận dự kiến là 7%, là bao nhiêu?

Trả lời:

Vấn đề này có thể được giải quyết bằng cách nhập các dữ liệu liên quan và tính FV.

$N = 15; I/Y = 7; PMT = -150; CPT → FV = 3,769.35$

Điều ngầm hiểu ở đây là PV = 0, thiết lập chức năng TVM.

Dòng thời gian cho các dòng tiền trong vấn đề này được minh họa trong hình dưới đây.

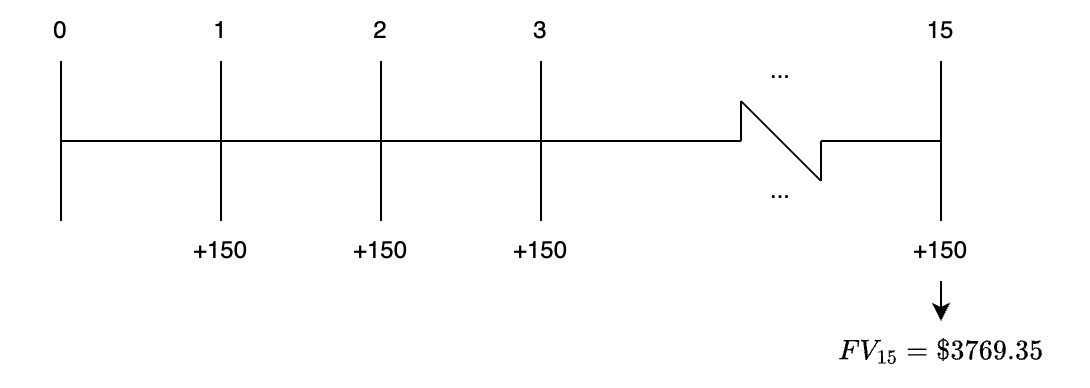
Như đã chỉ ra ở đây, tổng giá trị kép của các dòng tiền cá nhân trong niên kim thông thường 15 năm này là $3,769.35. Lưu ý rằng các khoản thanh toán niên kim tự nó lên tới $2,250 = 15 × $150, và số dư là lãi suất kiếm được với mức 7% mỗi năm.

Để tìm PV của một niên kim thông thường, chúng ta sử dụng dòng tiền tương lai, PMT, mà chúng ta đã sử dụng với các vấn đề niên kim FV, nhưng chúng ta chiết khấu các dòng tiền trở về hiện tại (thời gian = 0) thay vì ghép lãi chúng lên đến ngày kết thúc của niên kim.

Ở đây một lần nữa, biến PMT là một khoản thanh toán định kỳ đơn lẻ, không phải tổng của tất cả các khoản thanh toán (hoặc tiền gửi) trong niên kim. PVAO đo lường PV tập thể của một dòng tiền mặt đều nhau nhận được vào cuối mỗi kỳ ghép lãi trong một số kỳ hạn định trước, N, với một tỷ lệ lợi nhuận xác định, I/Y. Các ví dụ sau minh họa cách xác định PV của một niên kim thông thường bằng cách sử dụng máy tính tài chính.

Ví dụ: PV của niên kim thông thường

Giá trị hiện tại (PV) của một niên kim trả $200 mỗi năm vào cuối mỗi năm trong 13 năm tới với tỷ lệ chiết khấu 6% là bao nhiêu?

Trả lời:

Các khoản thanh toán diễn ra vào cuối năm, vì vậy niên kim này là một niên kim thông thường. Để giải quyết vấn đề này, nhập các thông tin liên quan và tính toán PV.

$N = 13; I/Y = 6; PMT = -200; CPT → PV = 1,770.54$

Số tiền $1,770.54 được tính ở đây đại diện cho số tiền mà một nhà đầu tư cần đầu tư hôm nay với tỷ lệ lợi nhuận 6% để tạo ra 13 dòng tiền cuối năm mỗi dòng $200.

Ví dụ: PV của niên kim thông thường bắt đầu sau t = 1

Giá trị hiện tại của bốn khoản thanh toán cuối năm $100 nếu khoản thanh toán đầu tiên được nhận sau ba năm kể từ hôm nay và tỷ lệ lợi tức thích hợp là 9% là bao nhiêu?

Câu trả lời:

Dòng thời gian cho dòng tiền này được hiển thị trong hình sau.

PV của một niên kim bắt đầu tại $t = 3$

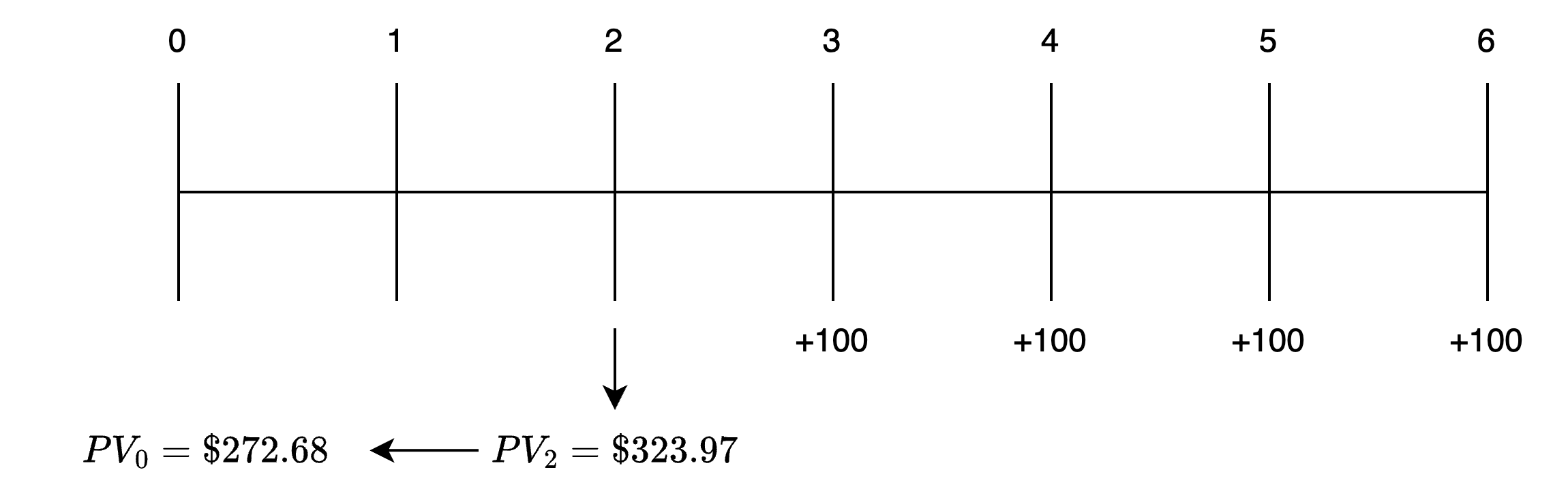
Bước 1: Tìm giá trị hiện tại của niên kim vào cuối năm thứ 2 ($PV_{2}$).

Nhập dữ liệu liên quan và giải cho $PV_{2}$.

$N = 4; I/Y = 9; PMT = -100; CPT → PV = PV_{2} = 323.97$

Bước 2: Tìm giá trị hiện tại của $PV_{2}$.

Nhập dữ liệu liên quan và giải cho $PV_{0}$.

$N = 2; I/Y = 9; PMT = 0; FV = -323.97; CPT → PV = PV_{0} = 272.68$

Trong giải pháp này, niên kim được coi là niên kim thông thường. PV được tính một giai đoạn trước khi khoản thanh toán đầu tiên bắt đầu, và chúng tôi chiết khấu $PV_{2} =$ $$323.97$ trong hai năm. Chúng tôi cần nhấn mạnh điểm quan trọng này. Chức năng PV niên kim trên máy tính của bạn được đặt ở chế độ "END" sẽ cung cấp cho bạn giá trị một giai đoạn trước khi niên kim bắt đầu. Mặc dù niên kim bắt đầu tại $t = 3$, chúng tôi chỉ chiết khấu kết quả trong hai giai đoạn để có giá trị hiện tại ($t = 0$).

Giá Trị Tương Lai của Niên Kim Đầu Kỳ

Đôi khi cần phải tính FV của một niên kim đầu kỳ ($FVA_{D}$), một niên kim mà các khoản thanh toán (hoặc gửi tiền) xảy ra vào đầu mỗi kỳ tính lãi kép. May mắn thay, máy tính tài chính của chúng ta có thể được sử dụng để làm điều này, nhưng với một sự điều chỉnh nhỏ - máy tính phải được đặt ở chế độ đầu kỳ (BGN). Để chuyển đổi giữa các chế độ BGN và END trên TI, nhấn [2nd] [BGN] [2nd] [SET]. Khi điều này được thực hiện, “BGN” sẽ xuất hiện ở góc trên bên phải của cửa sổ hiển thị. Nếu màn hình hiển thị chế độ mong muốn, nhấn [2nd] [QUIT]. Bạn sẽ thường muốn máy tính của mình ở chế độ niên kim thông thường (END), vì vậy hãy nhớ chuyển ra khỏi chế độ BGN sau khi làm việc với các bài toán niên kim đầu kỳ. Lưu ý rằng không có gì xuất hiện ở góc trên bên phải của cửa sổ hiển thị khi TI được đặt ở chế độ END. Cần đề cập rằng trong khi các khoản thanh toán của niên kim đầu kỳ được thực hiện hoặc nhận vào đầu mỗi kỳ, FV của một niên kim đầu kỳ được tính vào cuối kỳ cuối cùng.

Một cách khác để tính FV của một niên kim đầu kỳ là tính FV của một niên kim thông thường, và chỉ cần nhân kết quả $FV$ với $[1 + \text{tỷ lệ lãi kép định kỳ} (I/Y)]$. Về mặt ký hiệu, điều này có thể được biểu diễn như sau:

$$\text{FVA}_{D} = \text{FVA}_{O} \times (1 + I/Y)$$

Các ví dụ sau minh họa cách tính FV của một niên kim đầu kỳ.

Ví dụ: FV của một niên kim đầu kỳ

Giá trị tương lai của một niên kim trả $100 mỗi năm vào đầu mỗi năm trong ba năm tới, bắt đầu từ hôm nay, nếu các dòng tiền có thể được đầu tư với tỷ lệ hàng năm là 10% là bao nhiêu? Lưu ý trong dòng thời gian trong hình dưới đây rằng FV được tính vào cuối năm cuối cùng trong vòng đời của niên kim, năm thứ 3, mặc dù khoản thanh toán cuối cùng xảy ra vào đầu năm thứ 3 (cuối năm thứ 2).

Trả lời:

Để giải quyết vấn đề này, hãy đặt máy tính của bạn ở chế độ BGN ([2nd] [BGN] [2nd] [SET] [2nd] [QUIT] trên TI hoặc [g] [BEG] trên HP), sau đó nhập dữ liệu liên quan và tính FV:

$N = 3, I/Y = 10, PMT = 100, CPT → FV = 364.10$

FV của một Niên Kim Đầu Kỳ

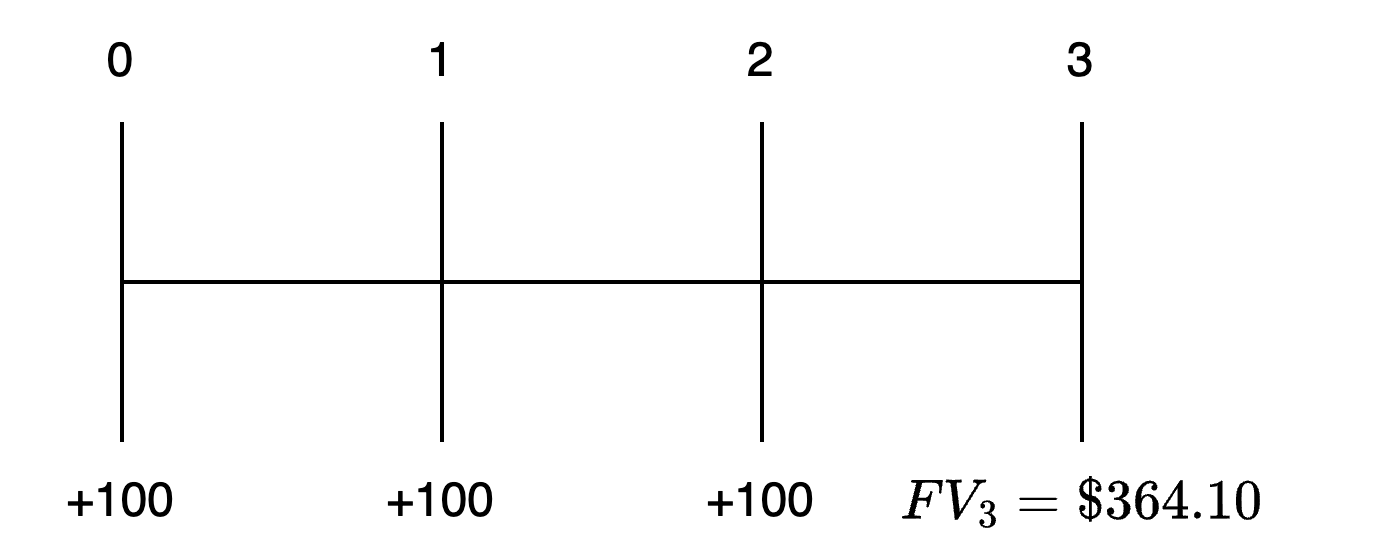
Ngoài ra, chúng ta có thể tính FV cho một niên kim thông thường và nhân nó với $1 + I/Y$. Để máy tính của bạn ở chế độ END, nhập các giá trị sau:

$N = 3, I/Y = 10, PMT = 100, CPT → FVA_{0} = 331.00$

$\text{FVA}_D = \text{FVA}_O \times (1 + I/Y) = 331.00 \times 1.10 = 364.10$

Giá Trị Hiện Tại của Niên Kim Đầu Kỳ

Trong khi ít phổ biến hơn so với các bài toán về niên kim thông thường, một số bài toán có thể yêu cầu bạn tìm giá trị hiện tại của niên kim đầu kỳ (PVAD). Sử dụng máy tính tài chính, điều này thực sự không phải là vấn đề lớn. Với niên kim đầu kỳ, có một kỳ chiết khấu ít hơn vì dòng tiền đầu tiên xảy ra tại t = 0 và do đó đã là giá trị hiện tại của nó. Điều này ngụ ý rằng, tất cả các yếu tố khác đều bằng nhau, giá trị hiện tại của niên kim đầu kỳ sẽ lớn hơn giá trị hiện tại của niên kim thông thường.

Như bạn sẽ thấy trong ví dụ tiếp theo, có hai cách để tính giá trị hiện tại của niên kim đầu kỳ. Cách thứ nhất là đặt máy tính ở chế độ BGN và sau đó nhập tất cả các biến liên quan (PMT, I/Y, và N) như bạn thường làm. Cách thứ hai, và dễ dàng hơn nhiều, là coi dòng tiền như một niên kim thông thường trong N kỳ gộp, và chỉ cần nhân giá trị hiện tại kết quả với [1 + tỷ lệ gộp định kỳ (I/Y)].

Biểu tượng hóa, điều này có thể được phát biểu như sau:

$$\text{PVA}_D = \text{PVA}_O \times (1 + I/Y)$$

Lợi thế của phương pháp thứ hai này là bạn để máy tính của mình ở chế độ END và không gặp rủi ro quên thiết lập lại. Bất kể quy trình nào được sử dụng, giá trị hiện tại tính được được đưa ra vào đầu kỳ đầu tiên, $t = 0$.

Ví dụ: PV của niên kim đầu kỳ

Với tỷ lệ chiết khấu là 10%, giá trị hiện tại của niên kim có các khoản thanh toán $200 vào đầu mỗi năm trong ba năm tới, bắt đầu từ hôm nay là bao nhiêu?

Trả lời:

Đầu tiên, hãy giải quyết vấn đề này bằng cách sử dụng chế độ BGN của máy tính. Đặt máy tính của bạn vào chế độ BGN ([2nd] [BGN] [2nd] [SET] [2nd] [QUIT] trên máy TI hoặc [g] [BEG] trên máy HP), nhập dữ liệu liên quan và tính PV.

$N = 3; I/Y = 10; PMT = -200; CPT → \text{PVA}_D = 547.11$

Dòng thời gian cho vấn đề này được hiển thị trong hình dưới đây.

PV của niên kim đầu kỳ

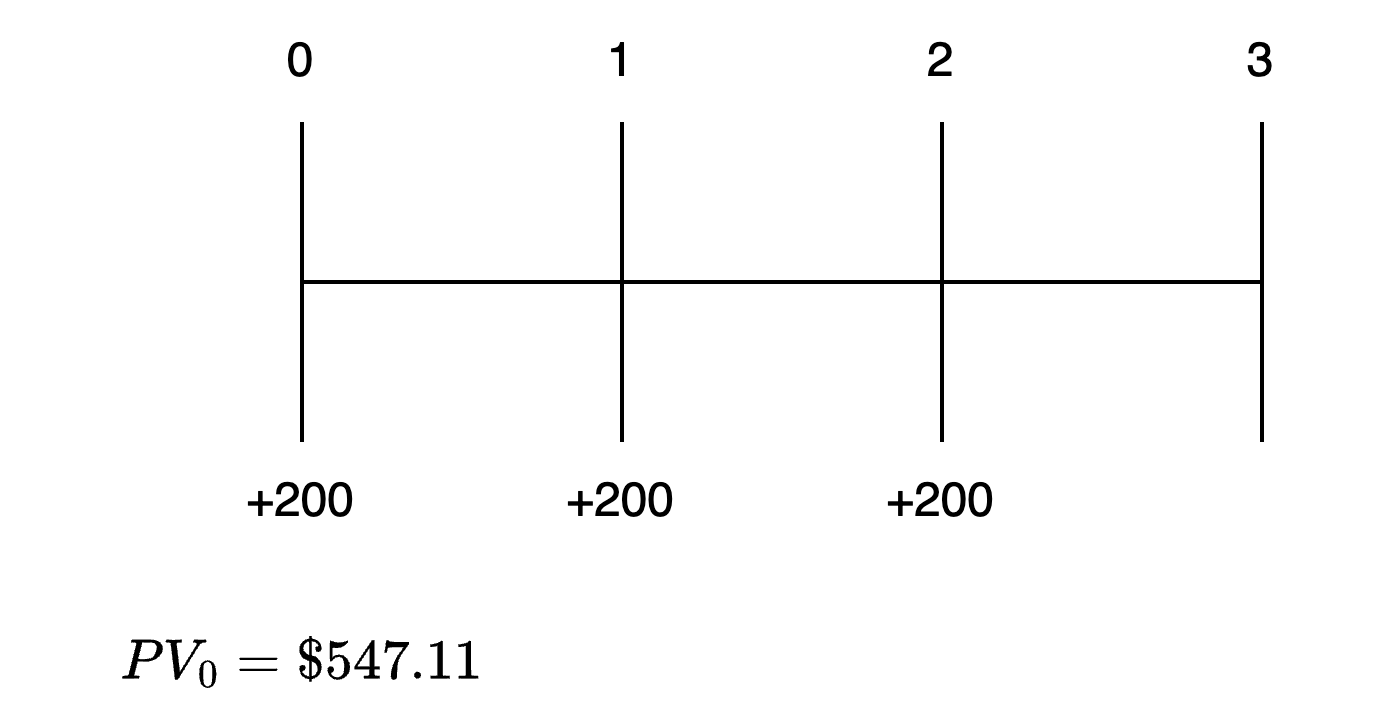
Ngoài ra, vấn đề này có thể được giải quyết bằng cách để máy tính của bạn ở chế độ END. Đầu tiên, tính PV của một niên kim thông thường trong 3 năm. Sau đó nhân PV này với (1 + I/Y). Để sử dụng cách tiếp cận này, hãy nhập các đầu vào liên quan và tính PV.

$N = 3; I/Y = 10; PMT = -200; CPT → \text{PVA}_O = 497.37$

$\text{PVA}_D = \text{PVA}_O \times (1 + I/Y) = 497.37 \times 1.10 = 547.11$

Giá trị hiện tại của niên kim vĩnh viễn (perpetuity)

Một niên kim vĩnh viễn (perpetuity) là một công cụ tài chính trả một khoản tiền cố định theo các khoảng thời gian nhất định trong một khoảng thời gian vô hạn. Về bản chất, niên kim vĩnh viễn là một loại niên kim vô thời hạn. Hầu hết các cổ phiếu ưu đãi là các ví dụ về niên kim vĩnh viễn vì chúng hứa hẹn trả lãi cố định hoặc cổ tức mãi mãi.

Bỏ qua các chi tiết toán học phức tạp, hệ số khấu trừ cho một niên kim vĩnh viễn chỉ đơn giản là một chia cho tỷ lệ hoàn vốn thích hợp (tức là, $1/r$). Do đó, chúng ta có thể tính toán Giá trị hiện tại (Giá trị hiện tại) (PV) của một niên kim vĩnh viễn.

$$\text{PV}_{perpetuity} = \frac{PMT}{I/Y}$$

Giá trị hiện tại của một niên kim vĩnh viễn là dòng tiền cố định theo kỳ chia cho tỷ lệ hoàn vốn kỳ hạn thích hợp.

Cũng giống như các ứng dụng giá trị thời gian của tiền (TVM) khác, phương trình $\text{PV}_{perpetuity}$ có thể được giải để tìm các ẩn số. Trên thực tế, bạn có thể giải cho bất kỳ biến số nào trong ba biến số liên quan, với điều kiện giá trị của hai biến số còn lại đã biết.

Ví Dụ: Giá trị hiện tại của một niên kim vĩnh viễn

Công ty Kodon phát hành cổ phiếu ưu đãi sẽ trả cổ tức hàng năm là $4.50 bắt đầu từ năm sau và dự định tuân theo chính sách cổ tức này mãi mãi. Với tỷ lệ hoàn vốn 8%, giá trị của cổ phiếu ưu đãi của Kodon hôm nay là bao nhiêu?

Trả lời: Vì giá trị của cổ phiếu là PV của tất cả các cổ tức trong tương lai, ta có:

$$PV_{perpetuity} = \frac{4.50}{0.08} = \$56.25$$

Do đó, nếu nhà đầu tư yêu cầu tỷ lệ hoàn vốn 8%, nhà đầu tư nên sẵn sàng trả $56.25 cho mỗi cổ phiếu ưu đãi của Kodon. Lưu ý rằng PV của một niên kim vĩnh viễn là giá trị của nó một kỳ trước kỳ thanh toán tiếp theo.

Ví Dụ: Giá trị hiện tại của một niên kim vĩnh viễn hoãn lại

Giả sử cổ phiếu ưu đãi của Kodon trong ví dụ trước dự kiến trả cổ tức đầu tiên sau bốn năm và không tích lũy (tức là không trả cổ tức trong ba năm đầu). Với tỷ lệ hoàn vốn yêu cầu là 8%, giá trị của cổ phiếu ưu đãi của Kodon hôm nay là bao nhiêu?

Trả lời: Như trong ví dụ trước,

$$PV_{perpetuity} = \frac{4.50}{0.08} = \$56.25,$$

nhưng vì cổ tức đầu tiên được trả vào $t = 4$, nên PV này là giá trị tại $t = 3$. Để có giá trị của cổ phiếu ưu đãi hôm nay, ta phải chiết khấu giá trị này trong ba kỳ:

$$\frac{56.25}{(1.08)^3} = \$44.65.$$

📝 Luyện tập

1. Số tiền một nhà đầu tư sẽ có sau 15 năm nếu đầu tư $1,000 hôm nay với lãi suất hàng năm 9% sẽ gần nhất là:

• A. $1,350.
• B. $3,518.
• C. $3,642.

2. Phải đầu tư bao nhiêu hôm nay, với lãi suất 8%, để tích lũy đủ trả một khoản nợ $10,000 đáo hạn sau bảy năm?

• A. $5,835.
• B. $6,123.
• C. $8,794.

3. Một nhà đầu tư vừa trúng xổ số và sẽ nhận được $50,000 mỗi năm vào cuối mỗi năm trong 20 năm tới. Với lãi suất 10%, giá trị hiện tại của số tiền thắng là gần nhất:

• A. $425,678.
• B. $637,241.
• C. $2,863,750.

4. Một nhà đầu tư sẽ nhận được một niên kim 15 năm, $8,000, với khoản thanh toán đầu tiên được nhận hôm nay. Với tỷ lệ chiết khấu 11%, giá trị hiện tại của niên kim này gần nhất là:

• A. $55,855.
• B. $57,527.
• C. $63,855.

5. Nếu $1,000 được đầu tư hôm nay và $1,000 được đầu tư vào đầu mỗi năm trong ba năm tới với lãi suất 12% (ghép hàng năm), số tiền mà nhà đầu tư sẽ có vào cuối năm thứ tư sẽ gần nhất là:

• A. $4,779.
• B. $5,353.
• C. $6,792.

6. Cổ phiếu ưu đãi của Terry Corporation dự kiến sẽ trả cổ tức hàng năm $9 mãi mãi. Nếu tỷ suất lợi nhuận yêu cầu trên các khoản đầu tư tương đương là 11%, một cổ phiếu ưu đãi của Terry nên trị giá:

• A. $81.82.
• B. $99.00.
• C. $122.22.

Dòng tiền không đều

Không hiếm khi có những ứng dụng trong đầu tư và tài chính doanh nghiệp mà cần phải đánh giá một dòng tiền không đều từ kỳ này sang kỳ khác. Dòng thời gian trong hình minh họa cho một dòng tiền như vậy.

Hình: Dòng thời gian cho dòng tiền không đều

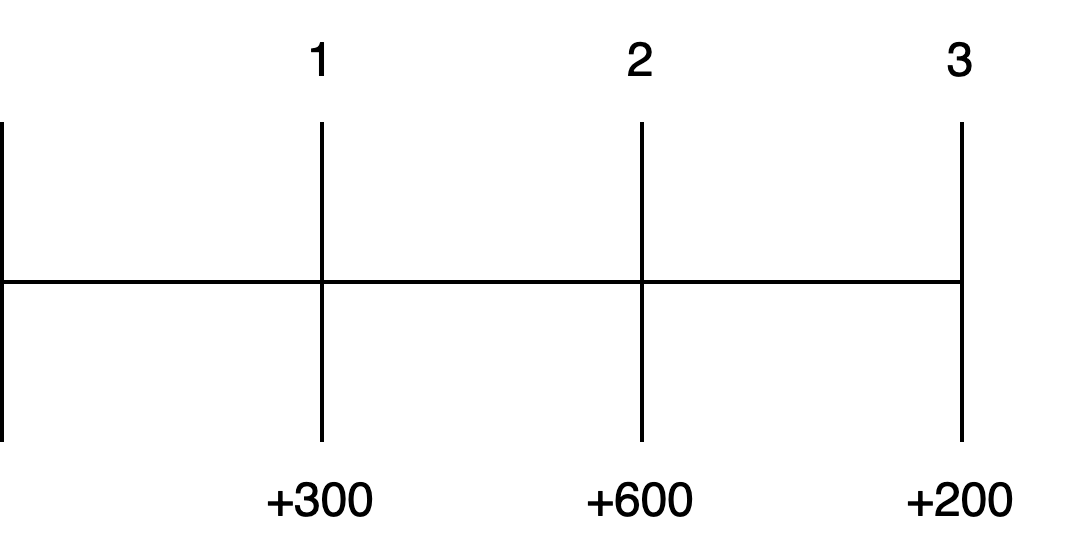
Dòng tiền ba năm này không phải là một niên kim vì các dòng tiền khác nhau mỗi năm. Về cơ bản, loạt dòng tiền không đều này không khác gì một loạt các dòng tiền đơn lẻ hàng năm. Do đó, để tìm PV hoặc FV của dòng tiền này, tất cả những gì chúng ta cần làm là tổng hợp PV hoặc FV của các dòng tiền riêng lẻ.

VÍ DỤ: Tính FV của một loạt dòng tiền không đều

Sử dụng tỷ lệ lợi nhuận là 10%, hãy tính giá trị tương lai của loạt dòng tiền không đều ba năm được mô tả ở trên vào cuối năm thứ ba.

Trả lời:

FV cho dòng tiền được xác định bằng cách đầu tiên tính FV của mỗi dòng tiền riêng lẻ, sau đó tổng hợp FV của các dòng tiền riêng lẻ.

$$FV_1: PV = -300; I/Y = 10; N = 2; CPT \rightarrow FV = FV_1 = 363$$ $$FV_2: PV = -600; I/Y = 10; N = 1; CPT \rightarrow FV = FV_2 = 660$$ $$FV_3: PV = -200; I/Y = 10; N = 0; CPT \rightarrow FV = FV_3 = 200$$ $$FV \text{ của dòng tiền} = \Sigma FV_{\text{các dòng tiền riêng lẻ}} = 1,223$$

VÍ DỤ: Tính PV của một loạt dòng tiền không đồng đều

Tính giá trị hiện tại của dòng tiền không đồng đều ba năm được mô tả trước đó bằng cách sử dụng tỷ lệ hoàn vốn 10%.

Trả lời:

Vấn đề này được giải quyết bằng cách tính PV của từng dòng tiền riêng lẻ, sau đó tổng hợp PV của các dòng tiền riêng lẻ, điều này cho ra PV của dòng tiền. Dấu hiệu của các dòng tiền vẫn được giữ nguyên.

$$PV_1: FV = 300; I/Y = 10; N = 1; CPT \rightarrow PV = PV_1 = -272.73$$ $$PV_2: FV = 600; I/Y = 10; N = 2; CPT \rightarrow PV = PV_2 = -495.87$$ $$PV_3: FV = 200; I/Y = 10; N = 3; CPT \rightarrow PV = PV_3 = -150.26$$ $$PV \text{ của dòng tiền} = \sum PV_{\text{các dòng tiền riêng lẻ}} = \$918.86$$

Giải Quyết Vấn Đề Giá Trị Thời Gian của Tiền Khi Kỳ Tính Lãi Khác Hàng Năm

Trong khi nền tảng khái niệm của các phép tính TVM không bị ảnh hưởng bởi kỳ tính lãi, tần suất tính lãi thường xuyên hơn có tác động đến việc tính FV và PV. Cụ thể, vì tăng tần suất tính lãi sẽ làm tăng tỷ lệ lãi suất thực, nó cũng tăng FV của một dòng tiền nhất định và giảm PV của một dòng tiền nhất định.

VÍ DỤ: Ảnh hưởng của tần suất tính lãi đến FV và PV

Tính FV một năm kể từ bây giờ của $1,000 hôm nay và PV của $1,000 sẽ nhận được một năm kể từ bây giờ sử dụng lãi suất hàng năm là 6% với một loạt các kỳ tính lãi.

Trả lời: Ảnh hưởng của Tần Suất Tính Lãi

$$\begin{array}{|l|c|c|c|c|} \hline \text{Tần Suất Tính Lãi} & \text{Tỷ Lệ Lãi Suất Mỗi Kỳ} & \text{Tỷ Lệ Hàng Năm Hiệu Quả} & \text{Giá Trị Tương Lai} & \text{Giá Trị Hiện Tại} \\ \hline \text{Hàng năm (m = 1)} & 6.000\% & 6.00\% & \$1,060.00 & \$943.396 \\ \text{Nửa năm (m = 2)} & 3.000\% & 6.090\% & \$1,060.90 & \$942.596 \\ \text{Hàng quý (m = 4)} & 1.500\% & 6.136\% & \$1,061.36 & \$942.184 \\ \text{Hàng tháng (m = 12)} & 0.500\% & 6.168\% & \$1,061.68 & \$941.905 \\ \text{Hàng ngày (m = 365)} & 0.016438\% & 6.183\% & \$1,061.83 & \$941.769 \\ \hline \end{array}$$

Có hai cách để sử dụng máy tính tài chính của bạn để tính PV và FV dưới các tần suất tính lãi khác nhau:

1. Điều chỉnh chế độ số kỳ mỗi năm (P/Y) trên máy tính của bạn để tương ứng với tần suất tính lãi (ví dụ: đối với hàng quý, P/Y = 4). CHÚNG TÔI KHÔNG KHUYẾN NGHỊ CÁCH NÀY!
2. Giữ máy tính ở chế độ tính lãi hàng năm (P/Y = 1) và nhập I/Y là tỷ lệ lãi suất mỗi kỳ tính lãi, và N là số kỳ tính lãi trong khoảng thời gian đầu tư. Cho m bằng số kỳ tính lãi mỗi năm, các công thức cơ bản cho dữ liệu đầu vào của máy tính được xác định như sau:

$$I/Y = \text{lãi suất hàng năm} / m$$ $$N = \text{số năm} × m$$

Các phép tính cho các giá trị FV và PV trong ví dụ trước:

$$PV_A: FV = -1,000; I/Y = 6 / 1 = 6; N = 1 × 1 = 1: CPT → PV = PV_A = 943.396$$ $$PV_S: FV = -1,000; I/Y = 6 / 2 = 3; N = 1 × 2 = 2: CPT → PV = PV_S = 942.596$$ $$PV_Q: FV = -1,000; I/Y = 6 / 4 = 1.5; N = 1 × 4 = 4: CPT → PV = PV_Q = 942.184$$ $$PV_M: FV = -1,000; I/Y = 6 / 12 = 0.5; N = 1 × 12 = 12: CPT → PV = PV_M = 941.905$$ $$PV_D: FV = -1,000; I/Y = 6 / 365 = 0.016438; N = 1 × 365 = 365: CPT → PV = PV_D = 941.769$$ $$FV_A: PV = -1,000; I/Y = 6 / 1 = 6; N = 1 × 1 = 1: CPT → FV = FV_A = 1,060.00$$ $$FV_S: PV = -1,000; I/Y = 6 / 2 = 3; N = 1 × 2 = 2: CPT → FV = FV_S = 1,060.90$$ $$FV_Q: PV = -1,000; I/Y = 6 / 4 = 1.5; N = 1 × 4 = 4: CPT → FV = FV_Q = 1,061.36$$ $$FV_M: PV = -1,000; I/Y = 6 / 12 = 0.5; N = 1 × 12 = 12: CPT → FV = FV_M = 1,061.68$$ $$FV_D: PV = -1,000; I/Y = 6 / 365 = 0.016438; N = 1 × 365 = 365: CPT → FV = FV_D = 1,061.83$$

VÍ DỤ: FV của một khoản đơn lẻ sử dụng tính lãi hàng quý

Tính FV của $2,000 hôm nay, năm năm kể từ hôm nay sử dụng lãi suất 12%, tính lãi hàng quý.

Trả lời:

Để giải quyết vấn đề này, nhập dữ liệu liên quan và tính FV:

$$N = 5 × 4 = 20; I/Y = 12 / 4 = 3; PV = -\$2,000; CPT → FV = \$3,612.22$$

E. Chứng minh việc sử dụng dòng thời gian trong mô hình hóa và giải quyết các vấn đề giá trị thời gian của tiền.

Trong hầu hết các vấn đề giá trị hiện tại (PV) mà chúng ta đã thảo luận, dòng tiền đã được chiết khấu về thời kỳ hiện tại. Trong trường hợp này, PV được nói là được đánh chỉ số tại t = 0, hoặc chỉ số thời gian là t = 0. Ví dụ, PV của một niên kim thông thường 3 năm được đánh chỉ số tại t = 0 được tính toán vào đầu năm 1 (t = 0). Đối lập với tình huống này là một niên kim thông thường 3 năm không bắt đầu cho đến năm thứ 4 và kéo dài đến năm thứ 6. Sẽ không có gì lạ khi muốn biết PV của niên kim này vào đầu năm thứ 4, trong trường hợp này chỉ số thời gian là t = 3. Dòng thời gian cho niên kim này được trình bày trong Hình dưới đây.

Hình: Đánh chỉ số Dòng Thời Gian khác với t = 0

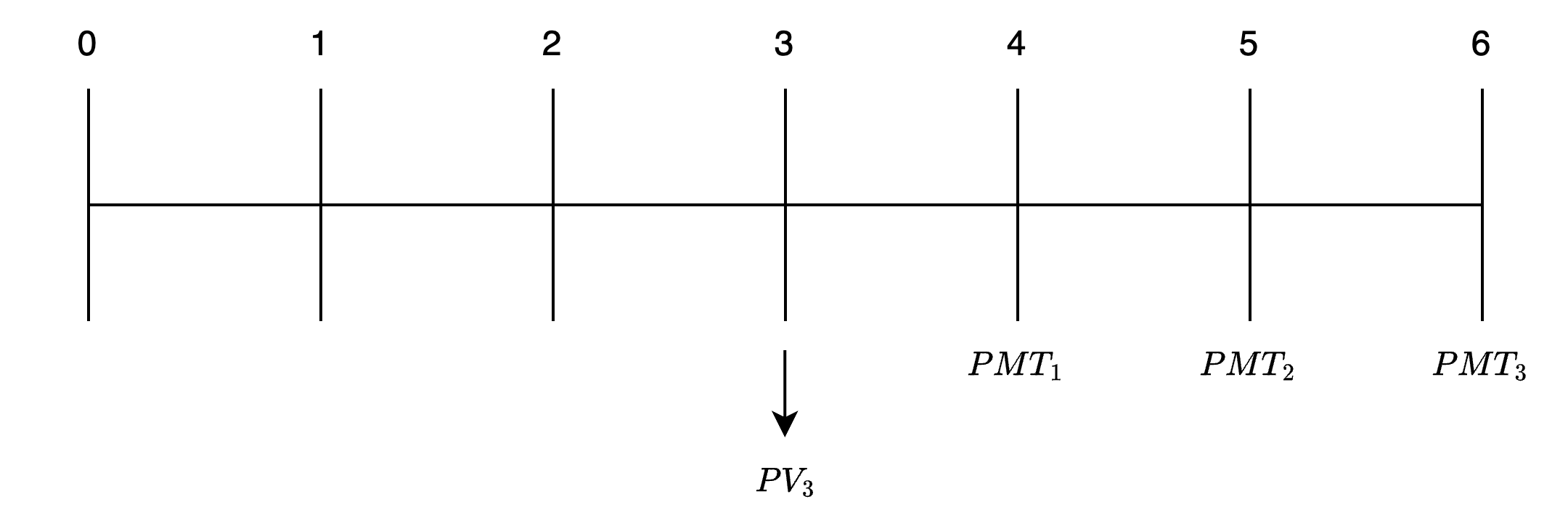
Các ví dụ sau đây sẽ minh họa cách tính toán I/Y, N, hoặc PMT trong các bài toán niên kim.

Ví dụ: Tính toán một khoản thanh toán niên kim cần thiết để đạt được FV cho trước

Với tỷ lệ lợi nhuận dự kiến là 7%, cần phải gửi bao nhiêu vào cuối mỗi năm trong 15 năm tới để tích lũy được $3,000?

Trả lời:

Để giải quyết vấn đề này, nhập ba giá trị đã biết liên quan và tính toán PMT.

$$N = 15; I/Y = 7; FV = +\$3,000; CPT → PMT = –\$119.38 \ \text{(bỏ qua dấu)}$$

Ví dụ: Tính toán khoản thanh toán khoản vay

Giả sử bạn đang xem xét việc xin một khoản vay $2,000 sẽ được hoàn trả bằng các khoản thanh toán cuối năm bằng nhau trong 13 năm tới. Nếu lãi suất hàng năm cho khoản vay là 6%, khoản thanh toán của bạn sẽ là bao nhiêu?

Trả lời:

Kích thước của khoản thanh toán cuối năm có thể được xác định bằng cách nhập các giá trị cho ba biến đã biết và tính toán PMT.

$$N = 13; I/Y = 6; PV = –2,000; CPT → PMT = \$225.92$$

Ví dụ: Tính toán số kỳ hạn trong một niên kim

Có bao nhiêu khoản thanh toán cuối năm $100 cần thiết để tích lũy được $920 nếu tỷ lệ chiết khấu là 9%?

Trả lời:

Số khoản thanh toán cần thiết có thể được xác định bằng cách nhập dữ liệu liên quan và tính toán N.

$$I/Y = 9\%; FV = \$920; PMT = –\$100; CPT → N = 7 \ \text{năm}$$

Sẽ mất bảy khoản thanh toán hàng năm $100, được gộp lại với lãi suất 9% hàng năm, để tích lũy giá trị đầu tư $920.

Lưu ý của Giáo sư

Hãy nhớ quy ước dấu. PMT và FV phải có dấu ngược nhau nếu không máy tính của bạn sẽ hiển thị thông báo lỗi.

Ví dụ: Tính toán số năm trong một niên kim thông thường

Giả sử bạn có một niên kim thông thường $1,000 với lợi nhuận 8%. Có bao nhiêu khoản rút cuối năm $150 hàng năm có thể được thực hiện?

Trả lời:

Số năm trong niên kim có thể được xác định bằng cách nhập ba biến liên quan và tính toán N.

$$I/Y = 8; PMT = 150; PV = –1,000; CPT → N = 9.9 \ \text{năm}$$

Ví dụ: Tính toán tỷ lệ lợi nhuận cho một niên kim

Giả sử bạn có cơ hội đầu tư $100 vào cuối mỗi năm trong 5 năm tới để đổi lấy $600 vào cuối năm thứ 5. Tỷ lệ lợi nhuận hàng năm trên khoản đầu tư này là bao nhiêu?

Trả lời:

Tỷ lệ lợi nhuận trên khoản đầu tư này có thể được xác định bằng cách nhập dữ liệu liên quan và giải quyết I/Y.

$$N = 5; FV = \$600; PMT = –100; CPT → I/Y = 9.13\%$$

Ví dụ: Tính toán tỷ lệ chiết khấu cho một niên kim

Bạn sẽ kiếm được tỷ lệ lợi nhuận bao nhiêu trên một niên kim thông thường yêu cầu khoản gửi $700 hôm nay và hứa hẹn sẽ trả $100 mỗi năm vào cuối mỗi năm trong 10 năm tới?

Trả lời:

Tỷ lệ chiết khấu trên niên kim này được xác định bằng cách nhập ba giá trị đã biết và tính toán I/Y.

$$N = 10; PV = –700; PMT = 100; CPT → I/Y = 7.07\%$$

Tài trợ một nghĩa vụ trong tương lai

Có nhiều ứng dụng của TVM (Giá trị thời gian của tiền) mà trong đó cần xác định kích thước của khoản tiền gửi phải được thực hiện trong một khoảng thời gian nhất định để đáp ứng một nghĩa vụ tài chính trong tương lai, chẳng hạn như thiết lập một chương trình tài trợ cho học phí đại học trong tương lai hoặc một chương trình hưu trí. Trong hầu hết các ứng dụng này, mục tiêu là xác định kích thước của khoản thanh toán hoặc khoản tiền gửi cần thiết để đạt được một mục tiêu tiền tệ cụ thể.

VÍ DỤ: Tính toán khoản thanh toán cần thiết để tài trợ cho một niên kim đầu kỳ

Giả sử bạn phải thực hiện năm khoản thanh toán hàng năm $1,000, bắt đầu từ đầu Năm 4 (cuối Năm 3). Để tích lũy tiền để thực hiện các khoản thanh toán này, bạn muốn thực hiện ba khoản thanh toán bằng nhau vào một tài khoản đầu tư, khoản đầu tiên sẽ được thực hiện một năm kể từ hôm nay. Giả sử tỷ suất lợi nhuận là 10%, số tiền của ba khoản thanh toán này là bao nhiêu?

Câu trả lời:

Dòng thời gian cho vấn đề niên kim này được hiển thị trong hình sau.

Tài trợ cho một niên kim đầu kỳ

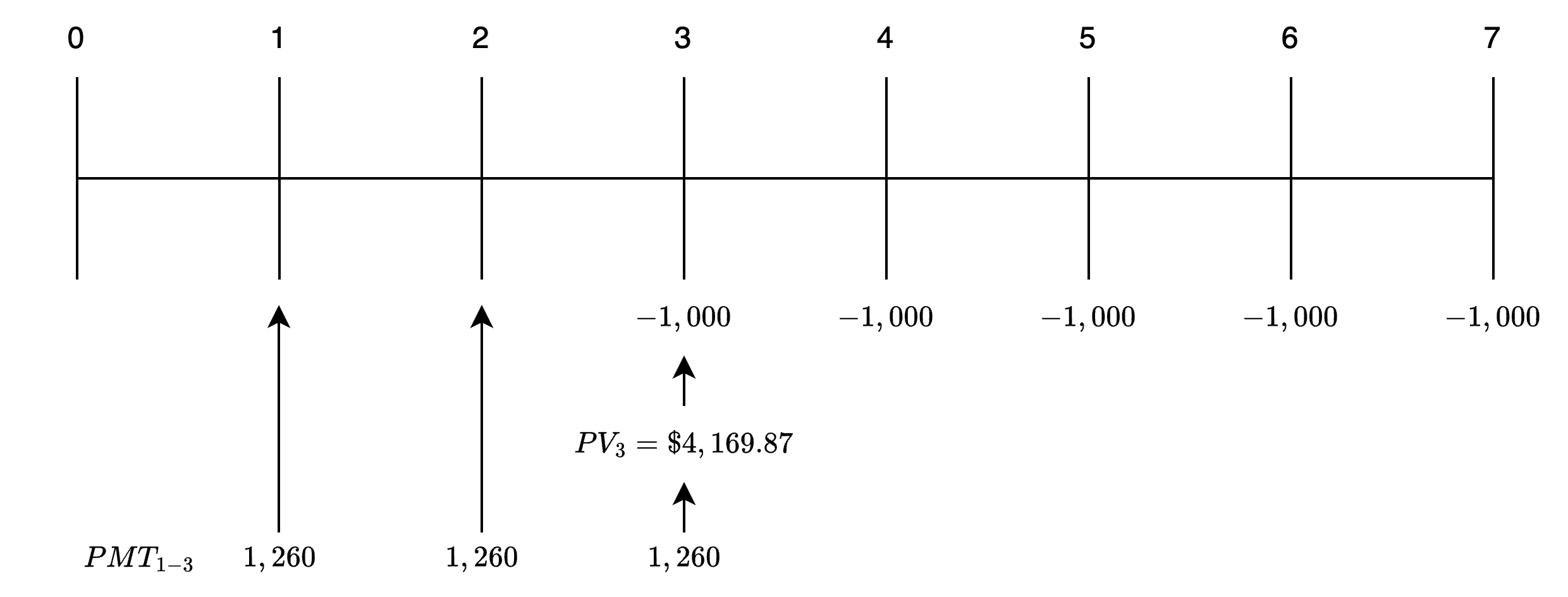
Bước đầu tiên trong loại vấn đề này là xác định số tiền phải có vào đầu Năm 4 (t = 3) để đáp ứng các yêu cầu thanh toán. Số tiền này là PV của một niên kim đầu kỳ 5 năm tại đầu Năm 4 (cuối Năm 3). Để xác định số tiền này, hãy đặt máy tính của bạn ở chế độ BGN, nhập dữ liệu liên quan và tính PV.

$$N = 5; I/Y = 10; PMT = -1,000; CPT → PV = PV_{3} = \$4,169.87$$

Ngoài ra, bạn có thể để máy tính của bạn ở chế độ END, tính toán PV của một niên kim thông thường 5 năm và nhân với 1.10.

$$N = 5; I/Y = 10; PMT = -1,000; CPT → PV = 3,790.79 × 1.1 = PV_{3} = \$4,169.87$$

Một cách thay thế thứ ba, với máy tính ở chế độ END, là tính giá trị t = 3 của bốn khoản thanh toán niên kim cuối cùng và sau đó cộng $1,000.

$$N = 4; I/Y = 10; PMT = -1,000; CPT → PV = 3,169.87 + 1,000 = \$4,169.87 = PV_{3}$$

$PV_{3}$ trở thành FV mà bạn cần có ba năm kể từ hôm nay từ ba khoản tiền gửi cuối năm bằng nhau. Để xác định số tiền của ba khoản thanh toán cần thiết để đáp ứng yêu cầu tài trợ này, hãy chắc chắn rằng máy tính của bạn ở chế độ END, nhập dữ liệu liên quan và tính PMT.

$$N = 3; I/Y = 10; FV = -4,169.87; CPT → PMT = \$1,259.78$$

Phần thứ hai của vấn đề này là một niên kim thông thường. Nếu bạn đã chuyển máy tính của mình sang chế độ BGN và không đặt lại chế độ END, bạn sẽ nhận được PMT là $1,145, điều này là không chính xác.

Mối Quan Hệ Giữa Giá Trị Hiện Tại, Giá Trị Tương Lai, và Dòng Tiền

Như chúng tôi đã giải thích trong phần thảo luận về niên kim và chuỗi dòng tiền không đều, tổng giá trị hiện tại của các dòng tiền là giá trị hiện tại của chuỗi. Tổng giá trị tương lai (tại thời điểm tương lai = n) của một chuỗi dòng tiền là giá trị tương lai của chuỗi dòng tiền đó.

Một cách hiểu về giá trị hiện tại của một chuỗi dòng tiền là số tiền cần phải gửi vào ngân hàng hôm nay để có thể thực hiện các khoản rút tiền trong tương lai và tiêu hết tài khoản bằng khoản rút cuối cùng. Hãy minh họa điều này với các dòng tiền $100 vào Năm 1, $200 vào Năm 2, $300 vào Năm 3, và lãi suất giả định là 10%.

Tính giá trị hiện tại của ba dòng tiền này như sau:

$$\frac{100}{1.1} + \frac{200}{1.1^2} + \frac{300}{1.1^3} = \$481.59$$

Nếu chúng ta gửi $481.59 vào một tài khoản có lãi suất 10%, vào cuối năm chúng ta sẽ có 481.59 × 1.1 = $529.75. Rút $100 sẽ còn lại $429.75.

Trong năm thứ hai, số tiền $429.75 sẽ tăng lên 429.75 × 1.1 = $472.73. Rút $200 sẽ còn lại $272.73.

Trong năm thứ ba, số tiền $272.73 sẽ tăng lên 272.73 × 1.1 = $300, để khoản rút cuối cùng là $300 sẽ làm rỗng tài khoản.

Cách hiểu về giá trị tương lai của một chuỗi dòng tiền cũng rất đơn giản. Giá trị tương lai trả lời câu hỏi, "Sẽ có bao nhiêu tiền trong tài khoản khi khoản gửi cuối cùng trong chuỗi được thực hiện?" Sử dụng ba dòng tiền $100, $200, và $300 cùng lãi suất 10%, chúng ta có thể tính giá trị tương lai của chuỗi này như sau:

$$100(1.1)^2 + 200(1.1) + 300 = \$641$$

Đây đơn giản là tổng giá trị tại t = 3 của mỗi dòng tiền. Lưu ý rằng giá trị tại t = 3 và giá trị hiện tại (t = 0) của chuỗi liên quan đến lãi suất, $481.59(1.1)^3 = 641$.

Dòng tiền $100 (khoản gửi) đến vào t = 1, vì vậy nó sẽ nhận lãi suất 10% gộp cho hai kỳ (đến t = 3). Dòng tiền $200 (khoản gửi) sẽ nhận lãi suất 10% giữa t = 2 và t = 3, và dòng tiền cuối cùng (khoản gửi) $300 được thực hiện tại t = 3, vì vậy $300 là giá trị tương lai (t = 3) của dòng tiền đó.

Chúng ta cũng có thể nhìn vào giá trị tương lai theo cách tài khoản tăng trưởng theo thời gian. Tại t = 1 chúng ta gửi $100, vì vậy tại t = 2 nó đã tăng lên $110 và khoản gửi $200 tại t = 2 làm cho số dư tài khoản là $310. Trong kỳ tiếp theo, số tiền $310 tăng lên 310 × 1.1 = $341 tại t = 3, và việc thêm khoản gửi cuối cùng $300 làm số dư tài khoản là $641. Đây tất nhiên là giá trị tương lai mà chúng ta đã tính ban đầu.

GHI CHÚ CỦA GIÁO SƯ

Cách nhìn này về giá trị tương lai của một chuỗi dòng tiền cho thấy một cách nhanh chóng để tính giá trị tương lai của một chuỗi dòng tiền không đều. Quá trình đã được mô tả trước đó để tính giá trị tương lai của một chuỗi các khoản thanh toán cuối kỳ có thể được viết dưới dạng toán học như sau: [(100 × 1.1) + 200] × 1.1 + 300 = 641, và đây có thể là một cách nhanh chóng để giải một số bài toán giá trị tương lai.

Lưu ý rằng các câu hỏi về giá trị tương lai của một niên kim trả trước đề cập đến số tiền trong tài khoản một kỳ sau khi khoản tiền gửi cuối cùng được thực hiện. Nếu ba khoản tiền gửi được xem xét ở đây được thực hiện vào đầu mỗi kỳ (tại t = 0, 1, 2) thì số tiền trong tài khoản vào cuối ba năm (t = 3) sẽ cao hơn 10% (tức là, 641 × 1.1 = $705.10).

Nguyên tắc cộng dòng tiền đề cập đến thực tế rằng giá trị hiện tại của bất kỳ dòng tiền nào bằng tổng giá trị hiện tại của các dòng tiền đó. Có nhiều ứng dụng khác nhau của nguyên tắc này trong các bài toán giá trị thời gian của tiền. Nếu chúng ta có hai loạt dòng tiền, tổng giá trị hiện tại của hai loạt này sẽ bằng với giá trị hiện tại của hai loạt dòng tiền được cộng lại với nhau, thêm các dòng tiền sẽ được thanh toán tại cùng một thời điểm. Chúng ta cũng có thể chia một loạt dòng tiền bất kỳ cách nào chúng ta muốn, và giá trị hiện tại của các “mảnh” sẽ bằng giá trị hiện tại của loạt dòng tiền ban đầu.

VÍ DỤ: Nguyên tắc cộng tính

Một chứng khoán sẽ thực hiện các khoản thanh toán sau vào cuối bốn năm tới: $100, $100, $400 và $100. Tính giá trị hiện tại của các dòng tiền này bằng cách sử dụng khái niệm giá trị hiện tại của niên kim khi tỷ lệ chiết khấu thích hợp là 10%.

Trả lời:

Chúng ta có thể chia các dòng tiền như sau:

t = 1	t = 2	t = 3	t = 4
100	100	100	100	chuỗi dòng tiền #1
0	0	300	0	chuỗi dòng tiền #2
------	-------	-------	-------
$100	$100	$400	$100

Nguyên tắc cộng tính cho chúng ta biết rằng để tính giá trị hiện tại của chuỗi gốc, chúng ta có thể chỉ cần cộng các giá trị hiện tại của chuỗi #1 (một niên kim 4 kỳ) và chuỗi #2 (một khoản thanh toán duy nhất sau ba kỳ).

Đối với niên kim: $N = 4; PMT = 100; FV = 0; I/Y = 10; CPT → PV = -\$316.99$

Đối với khoản thanh toán duy nhất: $N = 3; PMT = 0; FV = 300; I/Y = 10; CPT → PV = -\$225.39$

Tổng của hai giá trị này là $316.99 + 225.39 = \$542.38$.

Tổng của hai giá trị hiện tại này là giống nhau (ngoại trừ làm tròn) với tổng giá trị hiện tại của các khoản thanh toán của chuỗi gốc:

$$\frac{100}{1.1} + \frac{100}{1.1^2} + \frac{400}{1.1^3} + \frac{100}{1.1^4} = \$542.38$$

📝 Luyện tập

1. Một nhà phân tích ước tính rằng thu nhập của XYZ sẽ tăng từ $3.00 một cổ phiếu lên $4.50 một cổ phiếu trong vòng tám năm tới. Tỷ lệ tăng trưởng trong thu nhập của XYZ gần với:

• A. 4.9%.
• B. 5.2%.
• C. 6.7%.

2. Nếu đầu tư $5,000 vào một quỹ với tỷ suất sinh lợi là 12% mỗi năm, khoảng bao nhiêu năm sẽ cần để khoản đầu tư này đạt $10,000?

• A. 4 năm.
• B. 5 năm.
• C. 6 năm.

3. Một khoản đầu tư dự kiến sẽ tạo ra các dòng tiền lần lượt là $500, $200 và $800 vào cuối ba năm tới. Nếu tỷ suất sinh lợi yêu cầu là 12%, giá trị hiện tại của khoản đầu tư này gần với:

• A. $835.
• B. $1,175.
• C. $1,235.

4. Nếu đầu tư $10,000 vào hôm nay vào một tài khoản mà lãi suất là 9.5%, giá trị của các khoản rút đều có thể lấy ra từ tài khoản vào cuối mỗi năm trong năm năm tới nếu nhà đầu tư dự định rút hết tài khoản vào cuối thời gian là bao nhiêu?

• A. $2,453.
• B. $2,604.
• C. $2,750.

5. Với tỷ suất sinh lợi là 11%, số tiền cần phải đưa vào tài khoản đầu tư vào cuối mỗi năm trong 10 năm tới để tích lũy được $60,000 để trả cho việc học của con là gần với:

• A. $2,500.
• B. $3,588.
• C. $4,432.

6. Một nhà đầu tư sẽ nhận được một niên kim là $4,000 mỗi năm trong 10 năm. Khoản thanh toán đầu tiên sẽ được nhận sau năm năm kể từ hôm nay. Với tỷ lệ chiết khấu là 9%, giá trị hiện tại của niên kim này gần với:

• A. $16,684.
• B. $18,186.
• C. $25,671.

7. Một nhà đầu tư đang xem xét một ngôi nhà trị giá $150,000. Nếu phải đặt cọc 20% và số dư được tài trợ với lãi suất 9% trong 30 năm tới, khoản thanh toán thế chấp hàng tháng là bao nhiêu?

• A. $799.33.
• B. $895.21.
• C. $965.55.

References

• https://youssef-serghini.weebly.com/5-the-time-value-of-money.html